목차
<논문링크>
FCN 논문이 중요한 이유는 두 가지로 요약할 수 있다.
1.
앞으로 딥러닝 기반의 segmentation 논문들을 읽을 때, FCN 논문에서 언급되는 다양한 용어들이 자주 등장하게 된다.
2.
대부분의 딥러닝 기반 segmentation 모델들이 FCN 구조를 기반으로 하고 있다.
그만큼 Segmentation 분야에서 굉장히 중요한 논문이라고 할 수 있다.
22.09 기준 논문 인용 33,000회
0. Abstract
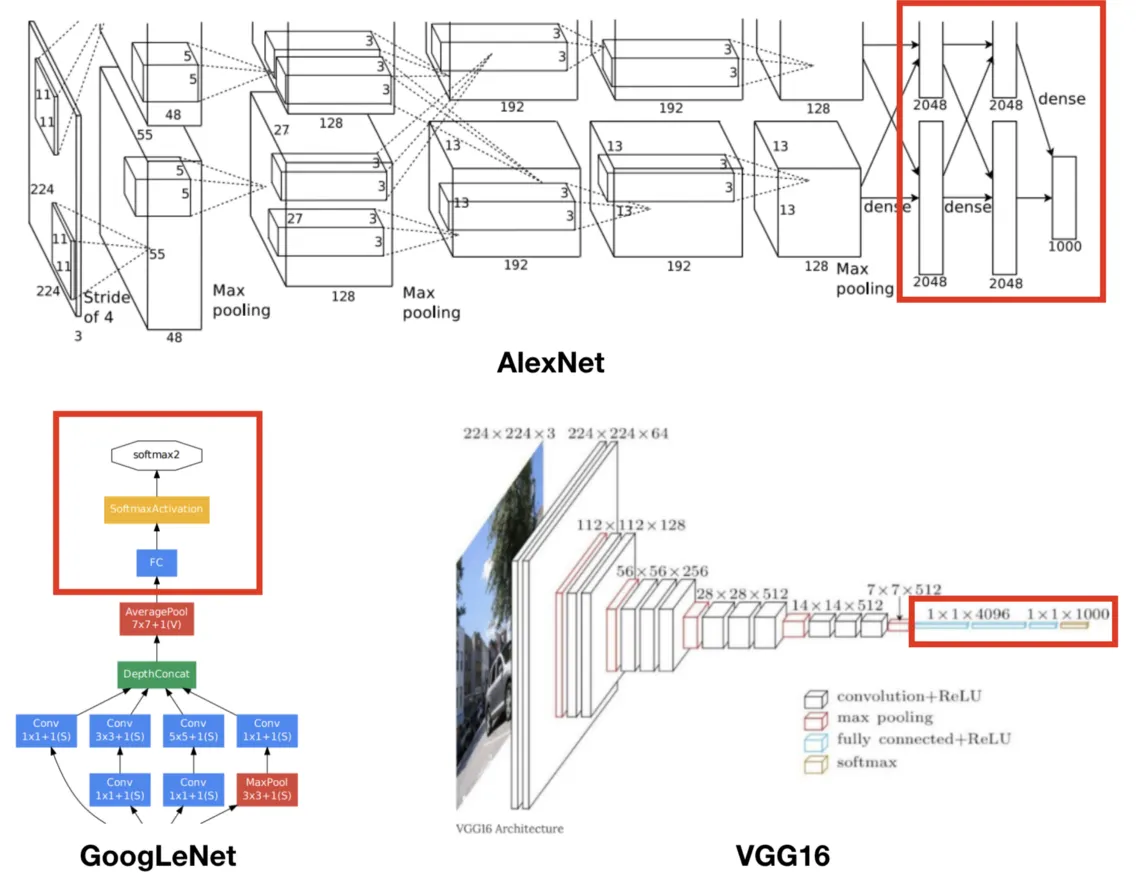
FCN(Fully Convolutional Networks)은 이미지 분류에서 우수한 성능을 보인 CNN 기반 모델(AlexNet, VGG16, GoogLeNet)을 Semantic Segmentation Task를 수행할 수 있도록 변형시킨 모델이다.
이러한 Image classification model to Semantic segmentation model은 다음 세 과정으로 표현된다.
•
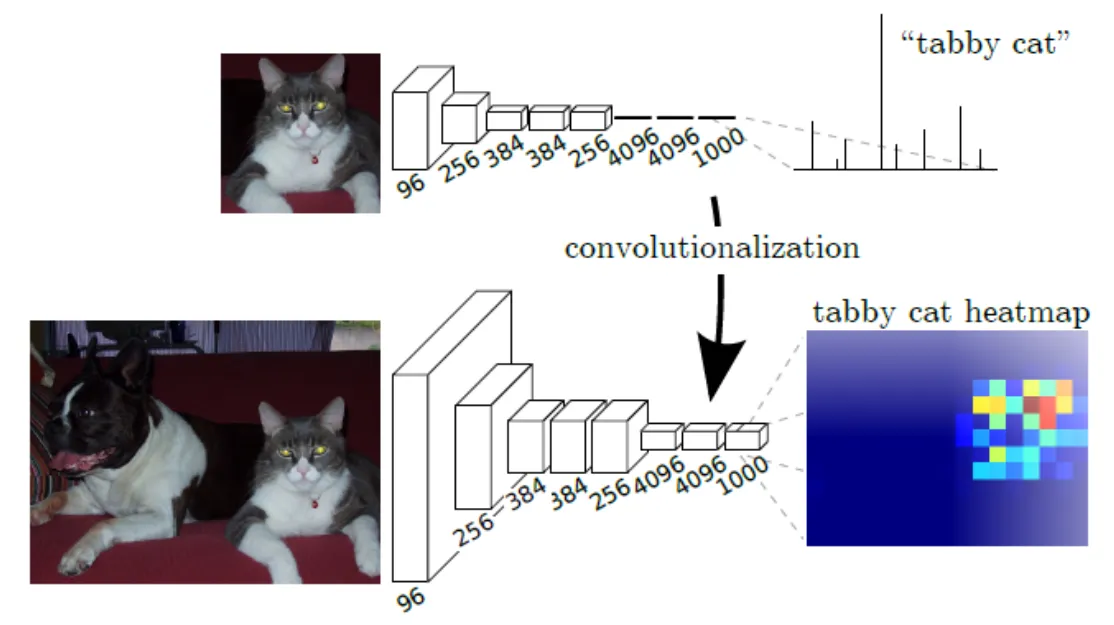
Convolutionalization
•
Deconvolution(Upsampling)
•
Skip architecture
1. Convolutionalization
Convolutionalization(컨볼루션화)라는 표현의 의미를 이해하기 위해서는 기존의 이미지 분류 모델들을 먼저 살펴볼 필요가 있다.
Image classification 모델들은 기본적으로 내부 구조와 관계없이 모델의 근본적인 목표를 위해 출력층이 Fully-connected(이하 FC) layer로 구성되어 있다.
이러한 구성은 네트워크의 입력층에서 중간부분까지 ConvNet을 이용하여 영상의 특징들을 추출하고 해당 특징들을 출력층 부분에서 fc를 이용해 이미지를 분류하기 위함이다.
그런데, Semantic Segmentation 관점에서 FC layer가 갖는 한계점이 있다.
FC layer의 한계점
1.
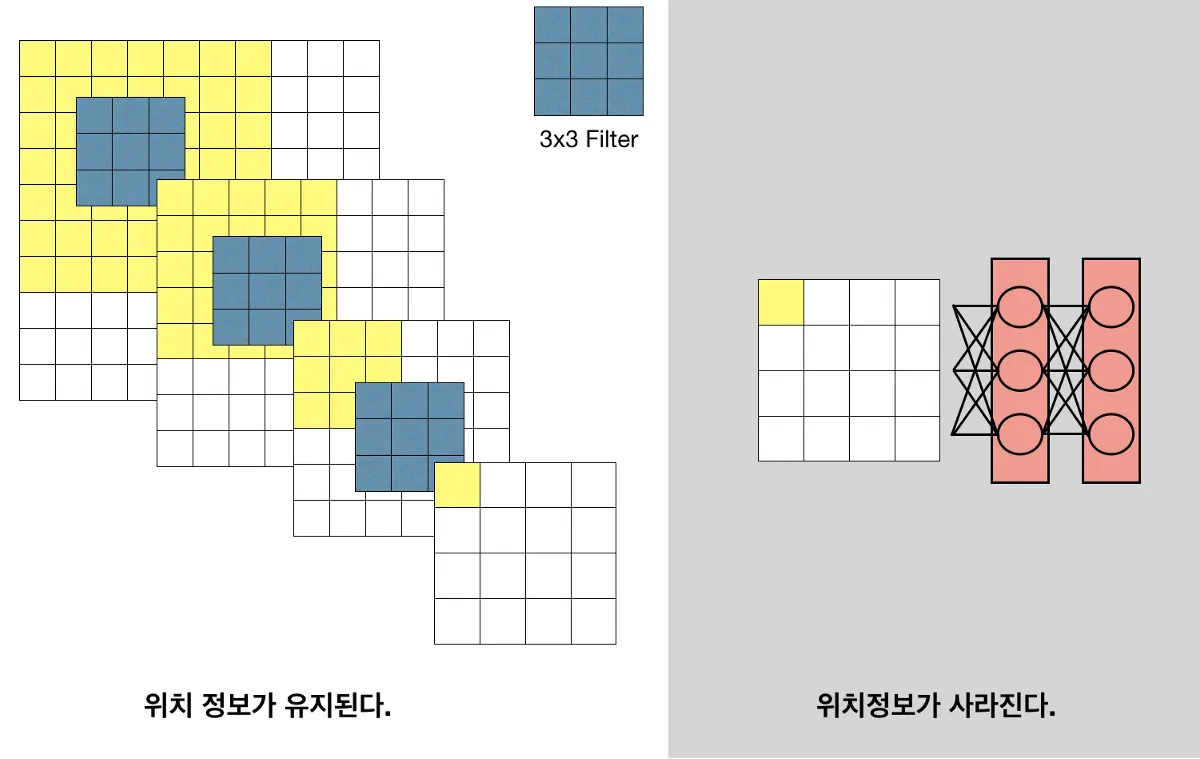
이미지의 위치정보가 사라진다.
Fully-Connected layer 연산 이후 Receptive field 개념이 사라진다.
2.
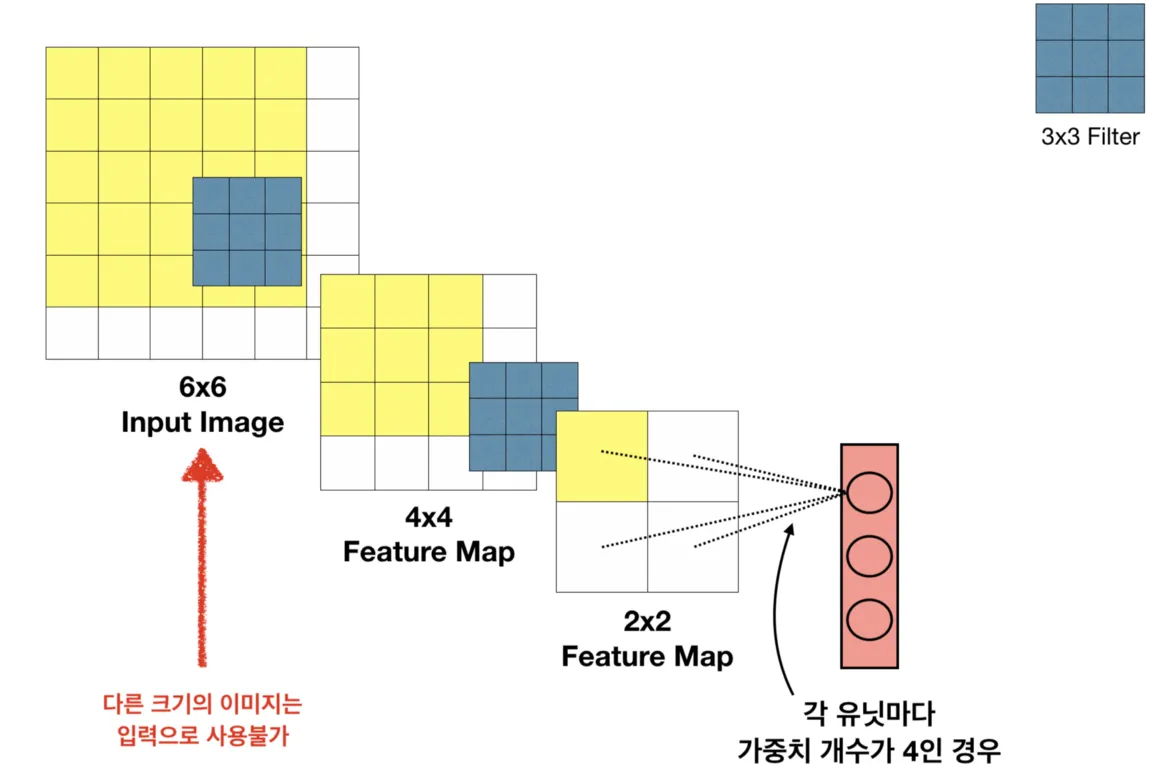
입력 이미지 크기가 고정된다.
Dense layer에 가중치 개수가 고정되어 있기 때문에 바로 앞 레이어의 Feature Map의 크기도 고정되며, 연쇄적으로 각 레이어의 Feature Map 크기와 Input Image 크기 역시 고정된다.
Segmentation의 목적은 원본 이미지의 각 픽셀에 대해 클래스를 구분하고 인스턴스 및 배경을 분할하는 것으로 위치 정보가 매우 중요하다.
따라서 이러한 FC-layer의 한계를 보완하기 위해 모든 FC-layer를 Conv-layer로 대체하는 방법을 택하였다.
Fully-connected layer는 입력의 모든 영역을 receptive field로 보는 필터의 Conv layer로 생각할 수 있다.
첫 번째 한계점에 대해 위의 그림을 보자.
2D 피쳐맵에 FC-layer는 1자형태로 펴진 것을 볼 수 있고, Convolution은 고양이에 대한 히트맵이 제대로 나온 것을 볼 수 있다. (정확히는 Fully Connected Layer를 적용할때, .view() 함수를 통해서 1차원의 Layer로 펼치고 거기에 FC Layer를 적용해서 위치 정보가 해쳐지게 된다.)
따라서 각 픽셀의 특징을 해당 위치에 보존할 수 있게 된다.
두 번째 한계점에 대해 위의 그림을 보자.
PyTorch의 두가지 인자에 대해서 입력 변수를 살펴보면,
•
Conv2d : 입력 채널
•
Linear : 입력 채널x높이x너비
즉, 이전 입력 (or 특징맵) 높이와 너비의 크기가 512x512로 고정되면 그에 맞는 하이퍼파라미터가 512x512xchannel로 설정되어야하고, 이때 입력이 256x256으로 바뀌면 계산이 되지가 않는다. 하지만, Conv2d는 입력 이미지의 크기에 따른 인자가 없어서 512x512로 학습이 된 이미지에 256x256의 입력이 들어와도 계산이 된다.
따라서 Convolution은 이미지 혹은 레이어의 크기에 대해서는 상관이 없게 된다.
2. Upsampling
Coarse map에서 Dense map을 얻는 몇 가지 방법이 있다
•
Interpolation
•
Deconvolution
•
Unpooling
•
Shift and stitch
물론 Pooling을 사용하지 않거나, Pooling의 stride를 줄임으로써 Feature map의 크기가 작아지는 것을 처음부터 피할수도 있다. 그러나, 이 경우 Receptive Field가 줄어들어 이미지 Context를 놓치게 된다.
또한, Pooling의 중요한 역할 중 하나는 특징맵의 크기를 줄임으로써 학습 파라미터의 수를 감소시키는 것인데, 이러한 과정이 사라지면 파라미터의 수가 급격히 증가하고 이로 인해 더 많은 학습시간을 요구하게 된다.
따라서, Coarse Feature map을 Dense map으로 Upsampling하는 방법을 고려해야 한다.
Bilinear Interpolation
10x10 이미지를 320x320 이미지로 확대하려면 어떻게 해야할까?
대표적인 방법이 바로 Bilinear interpolation이다. Bilinear interpolation을 이해하기 위해서는 Linear interpolation을 우선적으로 이해할 필요가 있다.
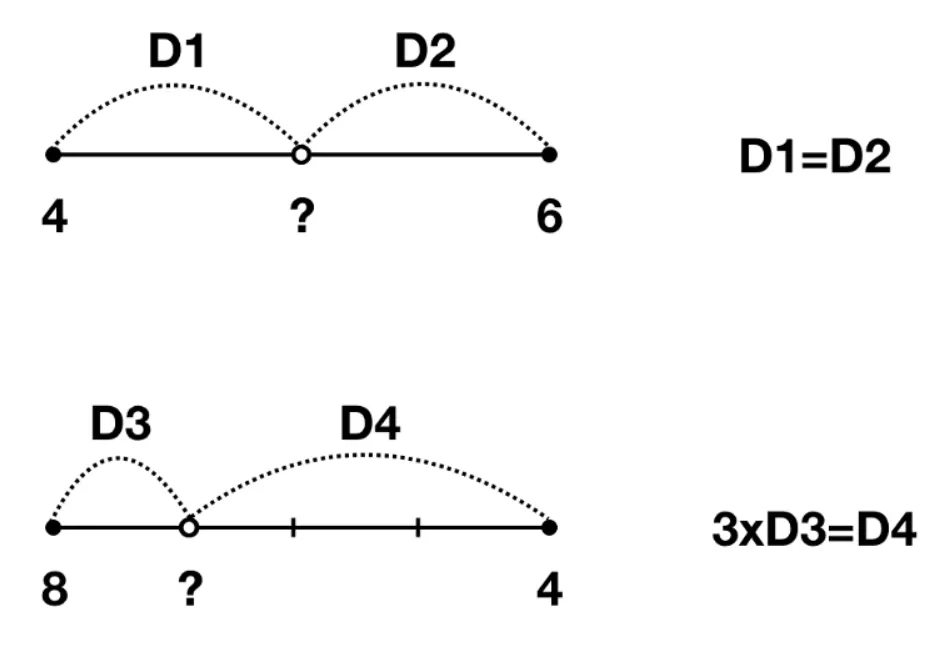
다음의 두 값을 예측해 보자.
위의 값은 5, 아래 값은 7 임을 어렵지 않게 예측할 수 있다. 이 처럼 두 지점 사이의 값을 추정할 때 직관적으로 사용하는 방법이 Linear interpolation이다.
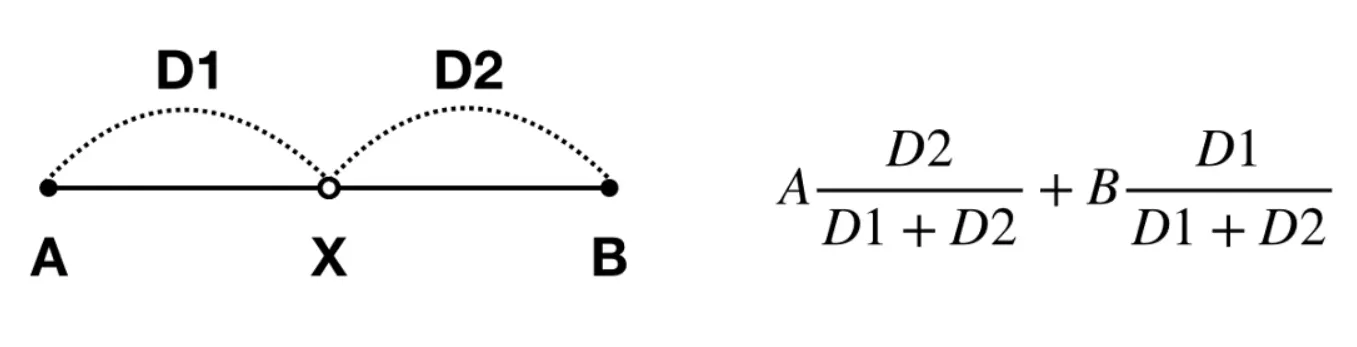
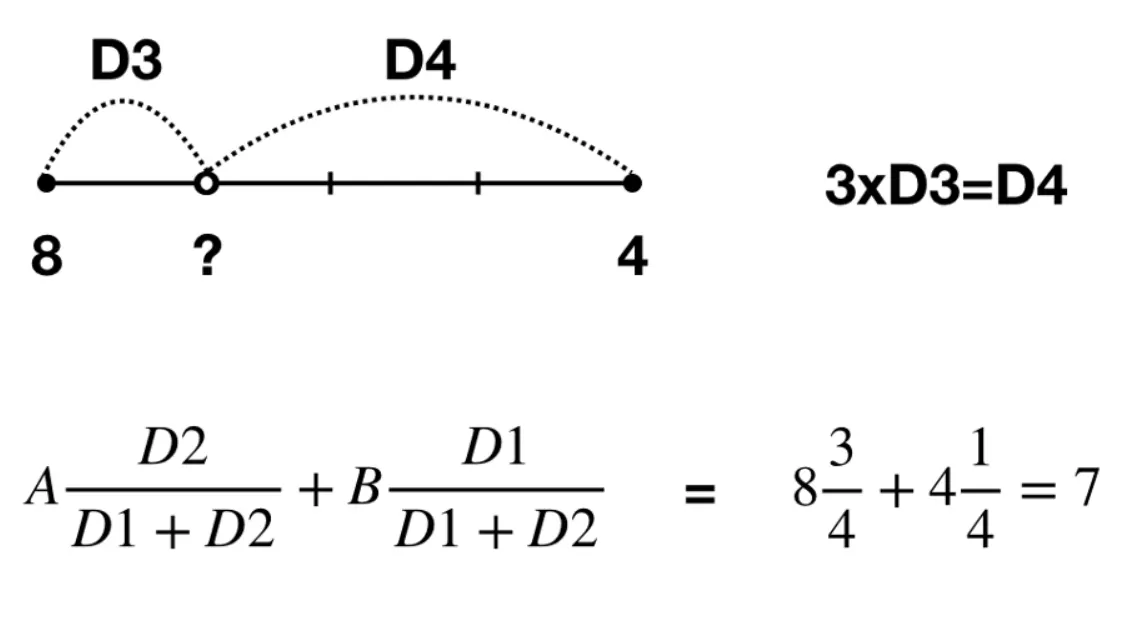
위의 추정 방식은 다음과 같이 식으로 표현할 수 있다.
식을 앞의 예제에 대입하면 다음과 같이 추정값을 쉽게 구할 수 있다.
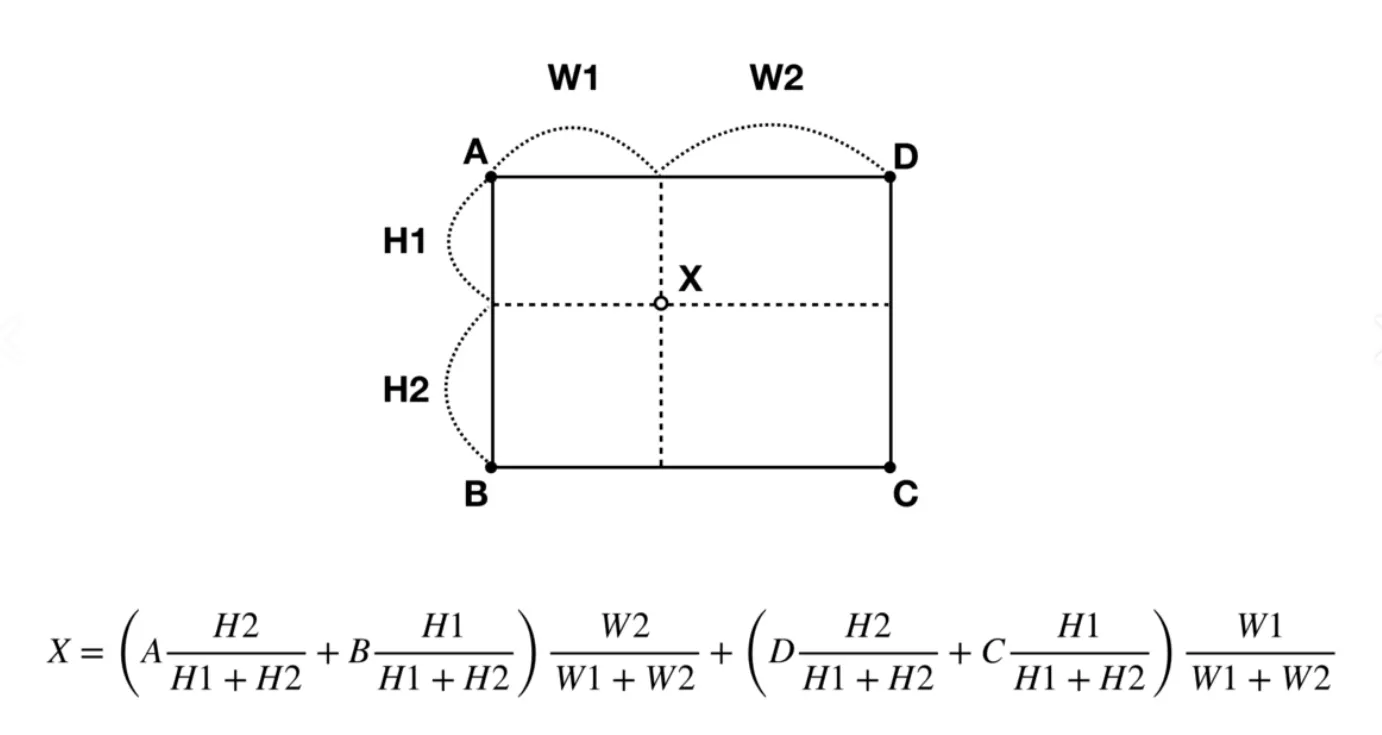
Bilinear interpolation은 이러한 1차원의 Linear interpolation을 2차원으로 확장한 것이다.
네 지점 A, B, C, D 사이의 임의의 점 X를 추정할 수 있다.
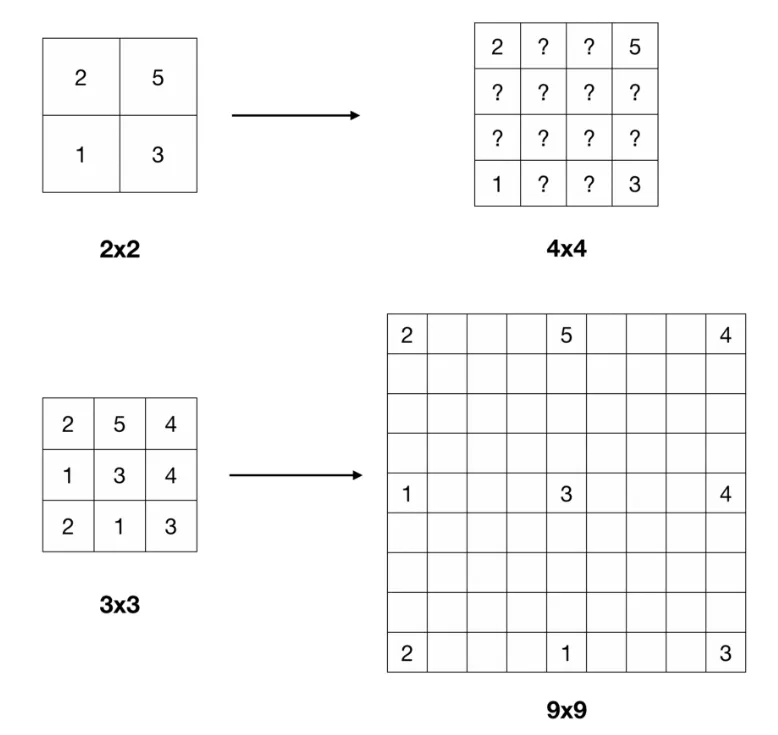
이제 우리는 다음과 같은 Feature map의 빈 영역을 추정할 수 있다.
양 끝의 수에 대해 등차수열 개념을 적용한다. 예시로 첫 번째 Feature Map의 2와 5사이에는 각각 3, 4가 들어간다.
Deconvolution
Upsampling하는 방법은 Convolution 연산을 통해서도 할 수 있다.
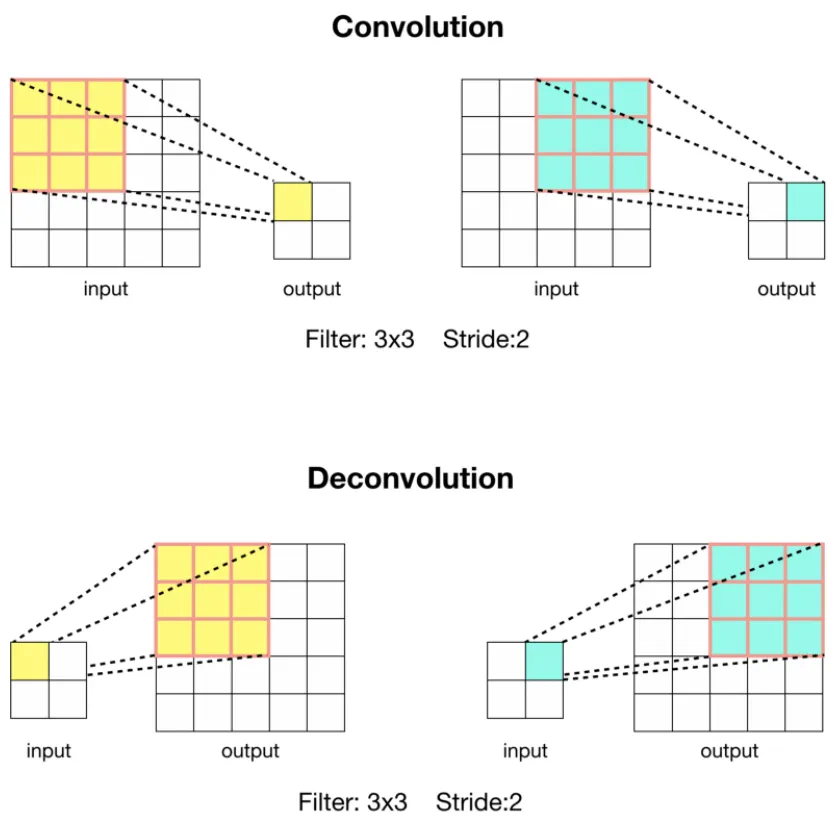
Stride가 2이상인 Convolution 연산의 경우 입력 이미지에 대해 크기가 줄어든 특징맵을 출력한다. 이것이 Down-sampling에 해당한다.
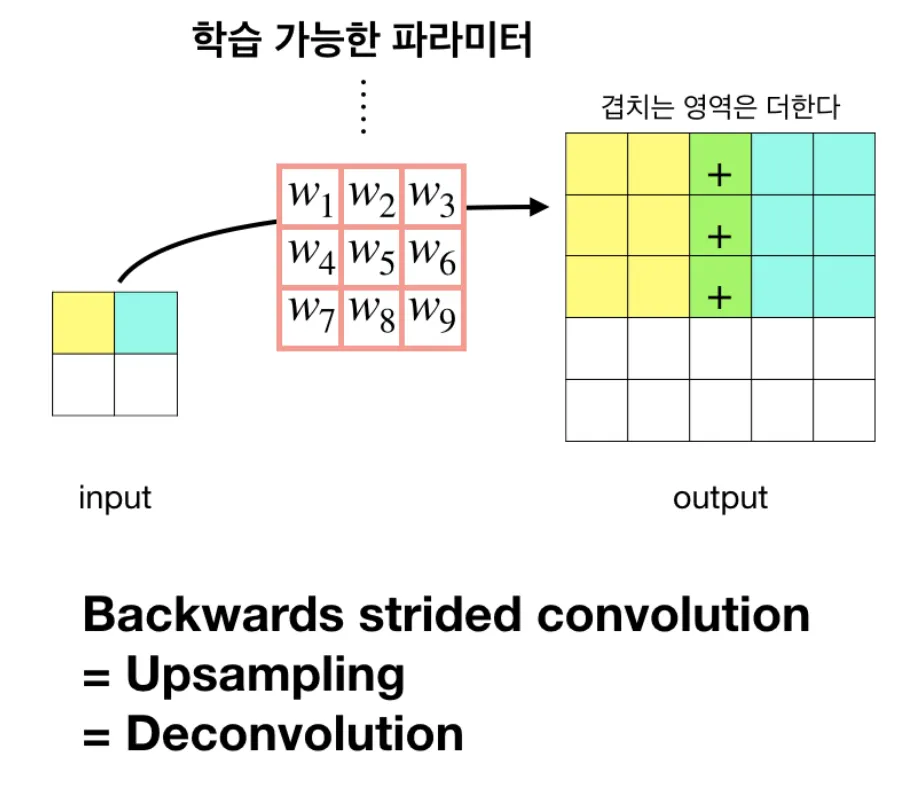
Convolution 연산을 반대로 할 경우 자연스럽게 Up-sampling 효과를 볼 수 있다. 또한, 이 때 사용하는 Filter의 가중치 값은 학습 파라미터에 해당한다.
Deconvolution은 Transposed Convolution, Backwards Convolution이라고도 한다.
3. Skip Connection
얕은 layer + 깊은 layer 결합 후 특징 추출을 목적으로 한다.
얕은 층은 일반적으로 복잡하지 않은 정보를 가지고, 깊은 층은 복잡한 정보를 가지기에
→ 앙상블 효과 & Maxpooling에 의해 잃어버리는 정보의 손실이 일어나기 전의 특징을 가져옴.