Gradient Vanishing을 막으려면
ResNet은 네트워크를 깊게 쌓으면서도 기울기 소실을 막을 수 있는 방법이 무엇일까 하는 의문에서 출발했다. 그렇다면 기울기 소실은 어떻게 막을 수 있을까?
연구에서는 Identity Mapping이라는 것에 주목했다. Identity Mapping은 간단히 말해서 입력을 어떤 특정한 함수에 들어가게 한 후 나온 출력이 입력과 동일한 것을 의미한다.
그런데 이를 CNN에 적용하는 것은 사실상 불가능하다. 왜냐하면 위 Identity Mapping이 가능하게 하는 것은 똑같은 값을 나오게 하는 활성함수인 가 적어도 처럼 선형 함수여야 한다는 것이다. 그런데 알다시피 CNN은 ReLU같은 비선형 함수를 활용할 수밖에 없다. 그래야 피쳐맵의 비선형 특징을 학습하여 다양한 특징을 추출할 수 있기 때문이다.
Residual
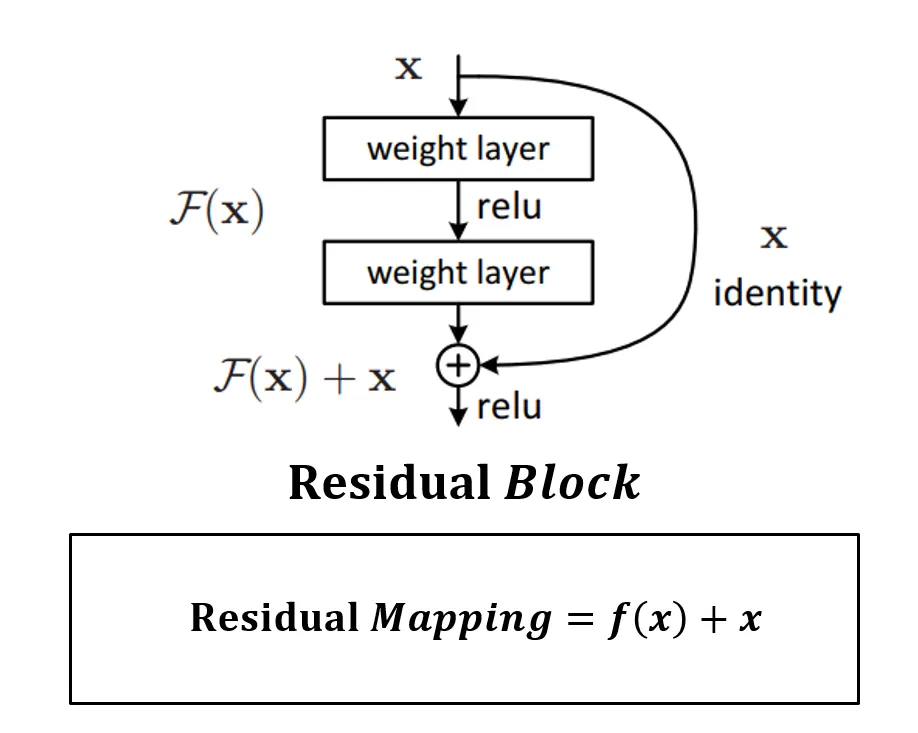
Residual을 이해하기 위해선 다음의 등식을 이해해야 한다.
위 수식에서 는 x라는 입력 데이터를 어떤 컨볼루션 데이터에 넣었을 때 그 출력값을 나오게하는 일종의 파라미터 함수를 의미한다.
는 가 그대로 보존되므로 기존에 학습한 정보를 보존하고, 거기에 추가적으로 학습하는 정보를 의미하게 된다. 즉, Output에 이전 레이어에서 학습했던 정보를 연결함으로써 해당 층에서는 추가적으로 학습해야 할 정보만을 Mapping, 학습하게 된다.
그리고 학습이 진행되어 layer의 depth가 깊어질 수록, 즉 학습이 많이 될수록 입력값 는 점점 출력값 에 근접하게 되어 추가 학습량 는 점점 작아져서 최종적으로 0에 근접하는 최소값으로 수렴되어야 할 것이다. 다시 말해 가 최소값(0)이 되도록 학습이 진행된다. 는 출력값과 입력값을 똑같게 해야 한다는 Identity Mapping 관점에서 잔차(residual)가 된다.
또 역전파를 수행하게 되면 를 미분해야 한다. 이를 미분하는 것은 곧 를 미분하는 것인데, 이 때 아무리 미분을 해도 1이 남기 때문에 기울기 소실 문제를 예방할 수 있다.
여기서 주의해야 할 점은 위의 identity 과정을 add할 때 배열의 차원수를 똑같이 맞춰 주어야 한다. 즉, 를 출력한 input layer와 Residual Block을 거친 값이 입력되는 Feature Map의 shape을 맞춰 주어야 한다. 그래야 값끼리 더하는 연산을 하는 add 연산을 할 수 있기 때문이다.
이 add 연산을 shortcut 또는 skip connection이라고 한다.
weight layer들을 통과한 F(x)와 weight layer들을 통과하지 않은 x의 합을 논문에서는 Residual Mapping 이라 하고, 위 그림의 구조를 Residual Block이라 하고, Residual Block이 쌓이면 Residual Network(ResNet)이라고 한다.