가중치 초깃값
가중치 초깃값은 신경망 학습에 있어서 매우매우 중요하다. 잘 설정한 초기 가중치가 신경망 전체의 성능을 좌우한다고해도 과언이 아니기 때문이다.
가중치 감소(weight decay)
가중치 감소 기법은 가중치 매개변수의 값이 작아지도록 학습하는 방법으로, 가중치 값을 작게 하여 오버피팅이 일어나지 않게 하는 것을 말한다.
→ 초깃값을 0으로 하면?
가중치 초깃값은 균일한 값으로 설정되면 안된다.
왜냐하면 오차역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문이다. 이렇게 되면 가중치를 여러개 갖는 의미가 없다. 따라서 가중치가 고른(대칭적인 구조) 상황을 막기 위해 가중치 초깃값은 균일하지 않은, 무작위의 값으로 설정되야 한다.
Xabier 초깃값
(Sigmoid에서 사용)
가중치의 초깃값은 은닉층 활성화값들에 영향을 미친다.
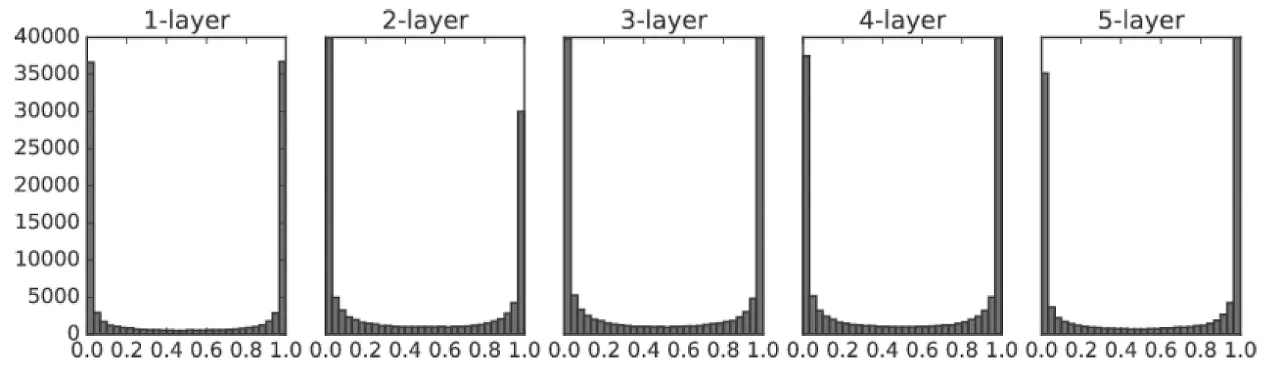
표준편차 1인 정규분포로 가중치를 초기화 했을 때의 각 층의 활성화값 분포
표준편차가 1인 정규분포로 초기 가중치 분포를 지정한 경우, 각 층의 활성화값들이 0과 1에 치우쳐져 있다. Sigmoid 함수는 값이 0 또는 1에 치우쳐지면 기울기가 0이 되기 때문에, 역전파의 기울기 값이 점점 작아지다 사라진다. (미분이 0이니까)
이러한 문제점을 기울기 소실(Gradient Vanishing)이라고 한다. 따라서 이 초기 가중치값은 층이 깊어지면 깊어질수록 제대로 학습을 하지 못한다.
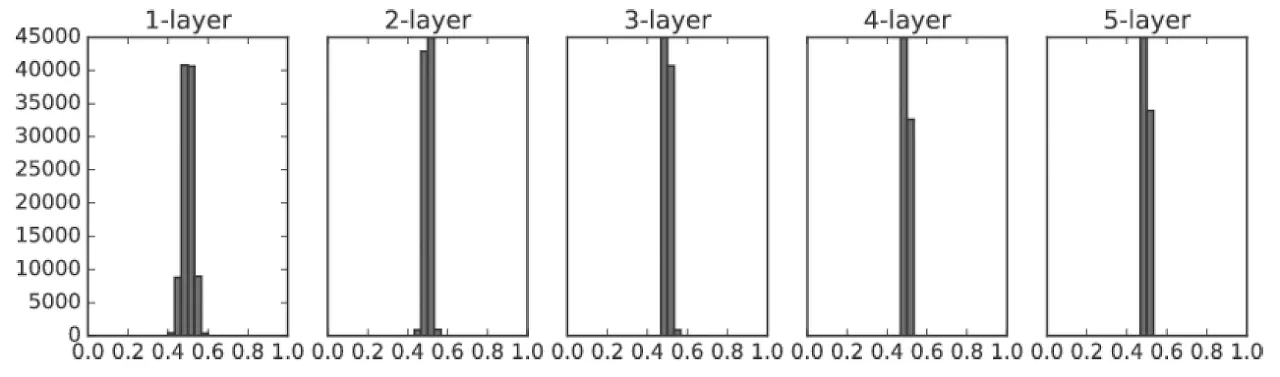
표준편차 0.01인 정규분포로 가중치를 초기화 했을 때의 각 층의 활성화값 분포
표준편차가 1인 경우와 달리 0 또는 1로 치우치진 않아 기울기 소실 문제가 일어나지는 않았지만 활성화값들이 0.5로 치우쳐진 것 또한 문제이다. 이는 다수의 뉴런의 거의 같은 값을 출력한다는 뜻으로 여러 뉴런을 갖는 이유가 없어지기 때문이다. 이러한 문제점을 표현력을 제한한다는 관점에서의 문제점이라고 한다.
결국 초기 가중치값은 활성화값들이 0 또는 1로 치우쳐지지 않게 하면서도 표현력을 제한하지 않도록 고르게 분포되도록 해야한다.
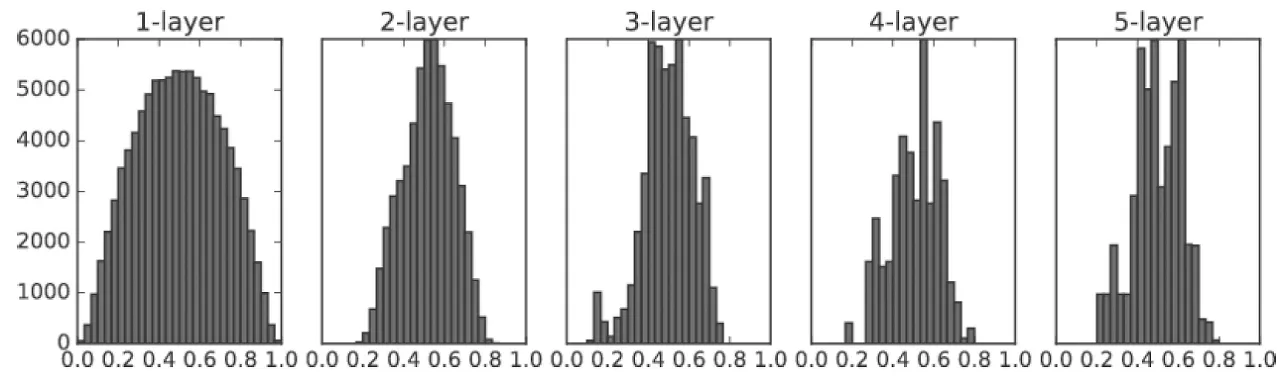
Xabier 초깃값을 이용할 때의 각 층의 활성화값 분포
Sigmoid에 대해서 활성화값들을 고르게 분포되게 해주는 초기 가중치값은 Xavier 초깃값으로, Xavier 초깃값은 일반적인 딥러닝 프레임워크들이 표준적으로 사용하고 있다.
Xavier 초깃값은 앞 계층의 노드가 n개일 때 표준편차가 인 분포를 사용한다.
Xavier 초깃값을 사용하면 앞 층에 노드가 많을수록 대상 노드의 초깃값으로 설정하는 가중치가 좁게 퍼진다. 쉽게 생각해 데이터가 적당히 퍼져있다는 말이다. 따라서 Xavier 초깃값은 Sigmoid 함수가 표현력의 제한도 받지 않으면서 효율적으로 학습할 수 있도록 한다.
추가적으로 위의 이미지를 보면 층이 깊어질수록 약간씩 일그러지는 형태를 볼 수 있는데, 이러한 일그러짐은 Sigmoid 함수 대신 tanh 함수를 사용하면 개선된다.
He 초깃값
(ReLU에서 사용)
Xavier 초깃값은 활성화 함수가 선형일 때 사용한다. Sigmoid 함수와 tanh 함수는 좌우가 대칭이라 중앙이 선형적이라고 볼 수 있기 때문에 Xavier 초깃값을 사용한다. 하지만 ReLU는 대칭적이지 않기 때문에 ReLU에 맞춰 초깃값을 설정해야한다. 이 초깃값이 He 초깃값이다.
사실 He 초깃값은 Xavier 초깃값과 크게 다르지는 않다. He 초깃값은 앞 계층의 노드가 n개일 때 표준편차가 인 정규분포를 사용하기 때문이다(Xavier의 2배). 이러한 이유는 ReLU는 음의 영역이 0이기 때문에 더 넓게 분포시켜야 했기 때문이라고 직감적으로 해석할 수 있다.
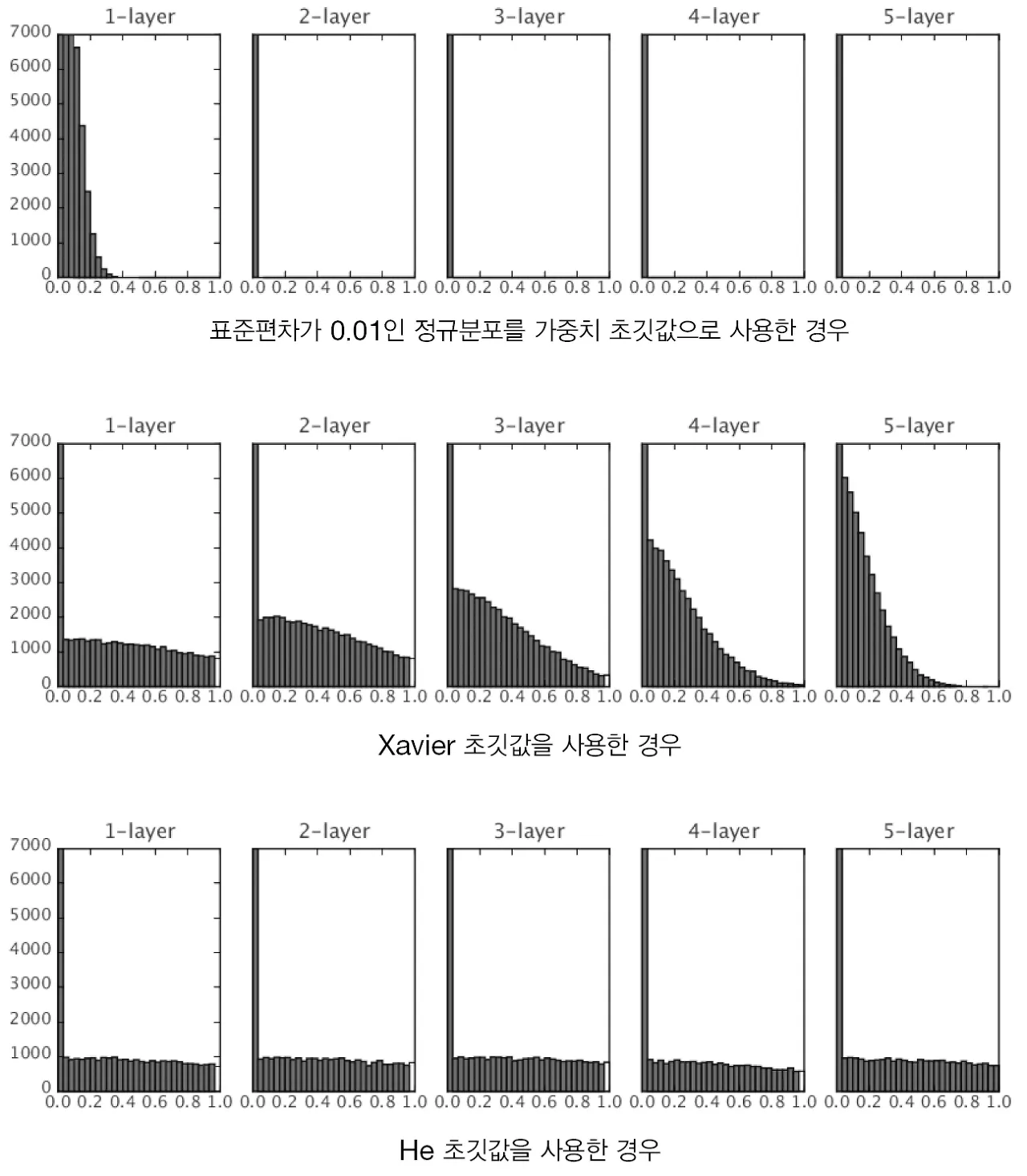
위의 그림을 보면 ReLU도 표준편차가 0.01인 경우 0으로 치우쳐진다. 또한 Xavier 초깃값을 사용하면 초반에는 고르게 분포되다가 층이 깊어질수록 치우치기 시작한다. 이는 층이 더 깊어지면 표준편차가 0.01인 경우와 같이 기울기 소실 문제가 발생한다.
He 초깃값을 보면 층이 깊어져도 균일하게 분포되어있기 때문에 학습이 잘 될 것으로 (역전파가 잘 될 것으로) 예상할 수 있다.
→ 결론적으로 현재까지는 Sigmoid나 tanh 등의 S자 모양 곡선 활성화 함수를 사용할 경우 Xavier 초깃값을 사용하고, ReLU를 사용할 때는 He 초깃값을 사용하는 것이 가장 좋은 가중치 초깃값이라고 볼 수 있다.