자료 구조(data structure)란 효율적으로 데이터를 관리하고 수정, 삭제, 탐색, 저장할 수 있는 데이터 집합을 말한다.
C++은 STL을 기반으로 전반적인 자료 구조를 가장 잘 설명할 수 있는 언어이다.
STL
C++의 표준 템플릿 라이브러리이자, 스택, 배열 등 데이터 구조의 함수를 제공
복잡도
복잡도는 알고리즘의 성능을 나타내는 척도이다.
•
시간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘의 수행 시간 분석
◦
알고리즘을 위해 필요한 연산의 횟수를 계산 가능.
•
공간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘의 메모리 사용량 분석
◦
알고리즘을 위해 필요한 메모리의 양을 계산 가능.
→ 동일한 기능을 수행하는 알고리즘이 있다면, 일반적으로 복잡도가 낮을수록 좋은 알고리즘이다.
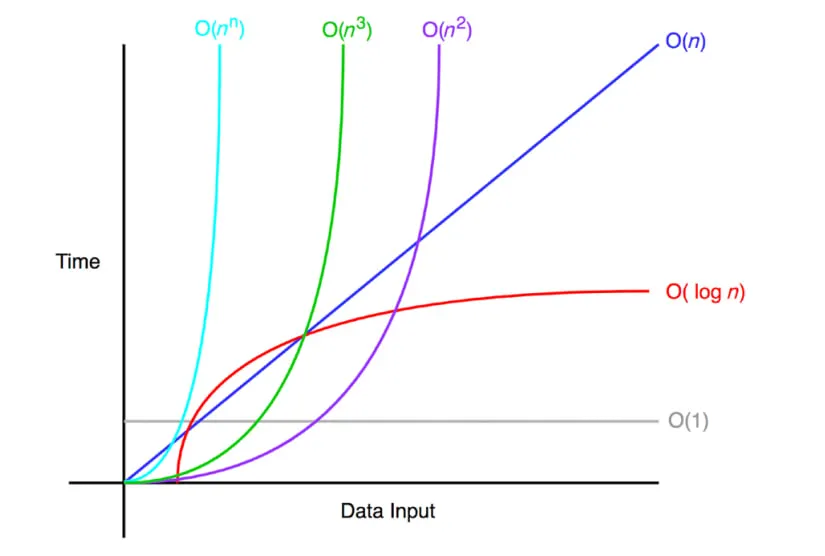
빅오 표기법(Big-O Notation)
가장 빠르게 증가하는 항만을 고려하는 표기법.
함수의 상한만을 나타내게 된다.
ex) 연산 횟수가 인 알고리즘일 경우
→ 빅오 표기법에서는 차수가 가장 큰 항만 남기므로 O()으로 표현된다.
1.
- 상수 시간
입력값이 증가해도 실행시간은 동일한 알고리즘.
index로 접근하여 바로 처리할 수 있는 연산 과정의 시간 복잡도 → 기본 연산 수라고 생각하면 편하다.
ex) stack의 push, pop
2.
- 로그 시간
연산이 한 번 실행될 때 마다 데이터의 크기가 절반 감소하는 알고리즘.
로그는 매우 큰 입력값에서도 크게 영향을 받지 않는 편이다. (log의 지수는 항상 2)
ex) binary search 알고리즘, tree 형태 자료구조 탐색
3.
- 선형 시간
입력값(N)이 증가함에 따라 실행 시간도 선형적으로 증가하는 알고리즘.
정렬되지 않은리스트에서 최대 또는 최솟값을 찾는 경우가 해당되며 모든 입렵값을 적어도 한 번 이상은 살펴봐야 한다.
ex) for문
4.
- 로그 선형 시간
O(N)의 알고리즘과 O(log N)의 알고리즘이 중첩된 형태. 대부분 효율이 좋은 알고리즘이 이에 해당 한다. 아무리 좋은 알고리즘이라 할지라도 n log n 보다 빠를 수 없다.
ex) 퀵/병합/힙 정렬
5.
- 이차 시간
입력 데이터 n만큼 반복하는데, 그 안에서 n만큼 또 반복할 때의 표기 방법이다.
데이터가 적을 때는 문제 없지만 많아질수록 수직 상승한다.
ex) 2중 for문, 삽입/버블/선택 정렬
6.
- 지수 시간
빅오 표기법 중 가장 느린 시간 복잡도로 주로 재귀적으로 수행하는 알고리즘이 이에 해당
ex) fibonacci 수열
7.
가장 느린 알고리즘으로 입력값이 조금만 커져도 계산이 어렵다.
요구사항에 따른 알고리즘 설계
문제에서 가장 먼저 확인해야 하는 내용은 시간제한(수행시간 요구사항)이다.
시간제한이 1초인 문제를 만났을 때, 일반적인 기준은 다음과 같다.
•
N의 범위가 500인 경우 : 시간복잡도 인 알고리즘을 설계하면 문제를 풀 수 있다.
•
N의 범위가 2,000인 경우 : 시간복잡도 인 알고리즘을 설계하면 문제를 풀 수 있다.
•
N의 범위가 100,000인 경우 : 시간복잡도 인 알고리즘을 설계하면 문제를 풀 수 있다.
•
N의 범위가 10,000,000인 경우 : 시간복잡도 인 알고리즘을 설계하면 문제를 풀 수 있다.
알고리즘 문제 해결 과정
일반적인 알고리즘 문제 해결 과정은 다음과 같다
1.
지문 읽기 및 컴퓨터적 사고
2.
요구사항(복잡도) 분석
3.
문제 해결을 위한 아이디어 찾기
4.
소스코드 설계 및 코딩
•
일반적으로 대부분 문제 출제자들은 핵심 아이디어를 캐치한다면, 간결하게 소스코드를 작성할 수 있는 형태로 문제를 출제한다!!
수행 시간 측정 - Python
import time
start_time = time.time() # 측정 시작
# 프로그램 소스코드
end_time = time.time() # 측정 종료
print("time :", end_time - start_time) # 수행 시간 출력
Python
복사
수행 시간 측정 소스코드
from random import randint
import time
# 배열에 10000개의 정수를 삽입
array = []
for _ in range(10000):
array.append(randint(1, 100)) # 1부터 100 사이의 랜덤한 정수
# 선택 정렬 프로그램 성능 측정
start_time = time.time()
# 선택 정렬 프로그램 소스코드
for i in range(len(array)):
min_index = i # 가장 작은 원소의 인덱스
for j in range(i + 1, len(array)):
if array[min_index] > array[j]:
min_index = j
array[i], array[min_index] = array[min_index], array[i] # 스와프
end_time = time.time() # 측정 종료
print("선택 정렬 성능 측정:", end_time - start_time) # 수행 시간 출력
# 배열을 다시 무작위 데이터로 초기화
array = []
for _ in range(10000):
array.append(randint(1, 100)) # 1부터 100 사이의 랜덤한 정수
# 기본 정렬 라이브러리 성능 측정
start_time = time.time()
# 기본 정렬 라이브러리 사용
array.sort()
end_time = time.time() # 측정 종료
print("기본 정렬 라이브러리 성능 측정:", end_time - start_time) # 수행 시간 출력
Python
복사
선택 정렬과 기본 정렬 라이브러리의 수행 시간 비교
Reference
•
이코테 with 파이썬 책 및 유튜브 강의 참고.