트리(Tree)는 계층형 트리 구조를 시뮬레이션하는 추상 자료형(ADT)으로, 루트값과 부모-자식 관계의 서브 트리로 구성되며, 서로 연결된 노드의 집합이다.
중요한 트리의 속성 중 하나는 재귀로 정의된(Recursively Defined) 자기 참조(Self-Referential) 자료구조라는 점이다.
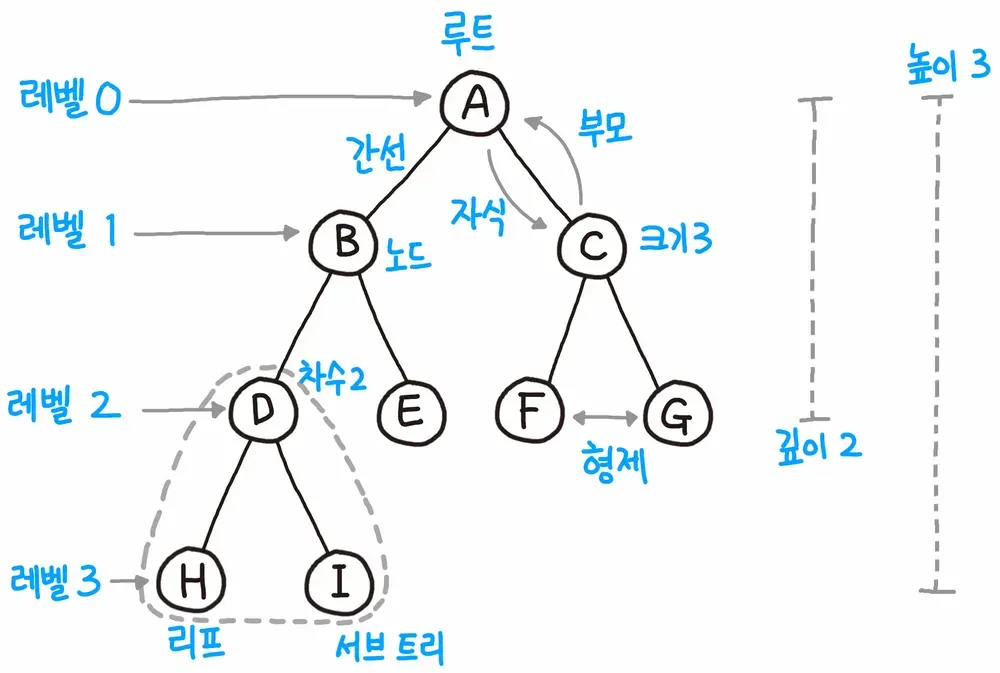
트리의 구조와 각 명칭
그래프와 트리의 차이점
“트리는 순환 구조를 갖지 않는 그래프이다.”
트리는 그래프와 달리 어떠한 경우에도 한 번 연결된 노드가 다시 연결되는 법이 없다. 이 외에도 단방향, 양방향을 모두 가리킬 수 있는 그래프와 달리, 트리는 부모 노드에서 자식 노드를 가리키는 단방향 뿐이다.
또한, 트리는 하나의 부모 노드를 가지며, 부모 또한 하나여야 한다.
이진 트리(Binary Tree)
트리 중에서도 가장 널리 사용되는 트리 자료구조는 이진 트리와 이진 탐색 트리(Binary Search Tree)이다.
먼저 각 노드가 m개 이하의 자식을 갖고 있으면, m-ary 트리(다항 트리, 다진 트리)라고 한다. 여기서 m=2일 경우, 즉 모든 노드의 차수가 2 이하일 때는 특별히 이진 트리라고 구분해서 부른다. 이진 트리는 왼쪽, 오른쪽 최대 2개의 자식을 갖는 형태이다.
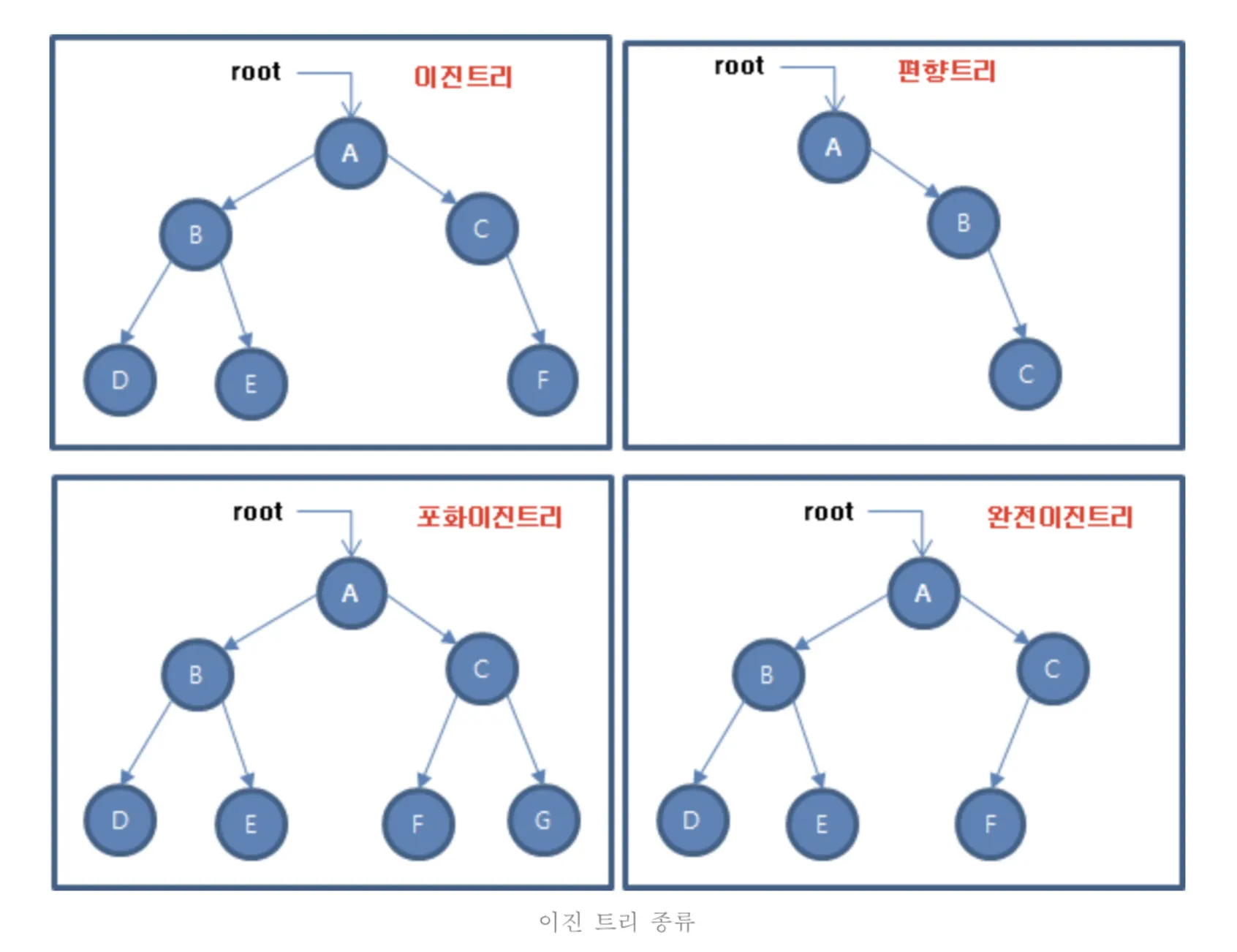
이진 트리의 유형
이진 탐색 트리(BST)
이진 탐색 트리란 정렬된 트리를 말하는데, 노드의 왼쪽 서브 트리는 그 노드의 값보다 작은 값들을 지닌 노드들로 이뤄져 있는 반면, 노드의 오른쪽 서브 트리는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이뤄져 있다. 이렇게 왼쪽과 오른쪽의 값들이 각각 값의 크기에 따라 정렬되어 있는 트리를 이진 탐색 트리라 한다.
이진 탐색 트리의 가장 훌륭한 점은 탐색 시 시간 복잡도가 이라는 점이다.
로그는 정말 마법과도 같은 수식인데, 1억 개의 아이템도 단 27번이면 모두 찾아낼 수 있다! ㄷㄷ