Greedy - 탐욕
그리디 알고리즘은 전체 최적을 찾기 위해 각 단계에서 로컬 최적의 선택을 하는 휴리스틱 문제 해결 알고리즘이다. 쉽게 얘기해 바로 눈앞의 이익만을 쫓는 알고리즘을 말한다.
그리디 알고리즘은 최적화 문제를 대상으로 한다. 최적해를 찾을 수 있으면 그것을 목표로 삼고, 찾기 어려운 경우에는 주어진 시간 내에 그런대로 괜찮은 해를 찾는 것을 목표로 삼는다. 물론 대부분의 문제들은 이런 로컬 최적해(Locally Optimum Solution)을 찾는 탐욕스런 방법으로는 문제를 해결할 수 없지만, 합리적인 시간 내에 최적해에 가까운 답을 찾을 수 있다는 점에서 매우 유용한 알고리즘이기도 하다.
그리디 알고리즘이 잘 작동하는 문제들은 탐욕 선택 속성(Greedy Choice Property)을 갖고 있는 최적 부분 구조(Optimal Substructure)인 문제들이다.
‘탐욕 선택 속성’은 항상 그 시점에 최적이라고 생각하는 것을 선택 하는 것을 말한다. 이때 지금까지 어떤 선택을 했느냐에 따라 현재 시점의 선택이 달라질 수 있으며, 미래의 선택이나 하위 문제에 대한 해결책 등은 전혀 고려하지 않는다.
‘최적 부분 구조’는 전체 문제의 최적해가 ‘부분 문제의 최적해로 구성’될 수 있는 경우를 말한다. 즉, 전체 문제를 작은 부분 문제로 나누어 각각의 부분 문제에서 최적의 해를 구한 후 이를 조합하여 전체 문제의 최적해를 구하는 것이다.
그리디 알고리즘의 단계
1.
문제의 최적해 구조를 결정한다.
2.
문제의 구조에 맞게 선택 절차를 정의합니다 : 선택 절차(Selection Procedure)
3.
선택 절차에 따라 선택을 수행한다.
4.
선택된 해가 문제의 조건을 만족하는지 검사합니다 : 적절성 검사(Feasibility Check)
5.
조건을 만족하지 않으면 해당 해를 제외한다.
6.
모든 선택이 완료되면 해답을 검사합니다 : 해답 검사(Solution Check)
7.
조건을 만족하지 않으면 해답으로 인정되지 않는다.
다이나믹 프로그래밍과의 차이점
→ 다이나믹 프로그래밍은 하위 문제에 대한 최적의 솔루션을 찾은 다음 이 결과들을 결합한 정보에 입각해 전체의 최적 솔루션을 선택하는 반면, 그리디는 각 단계마다 로컬 최적해를 찾는 문제로 접근해 문제를 더 작게 줄여나가는 형태로, 서로 반대 방향으로 접근하는 구조이다.
배낭 문제 (Knapsack Problem)
배낭 문제는 조합 최적화(Combinatorial Optimization)분야의 매우 유명한 문제이다.
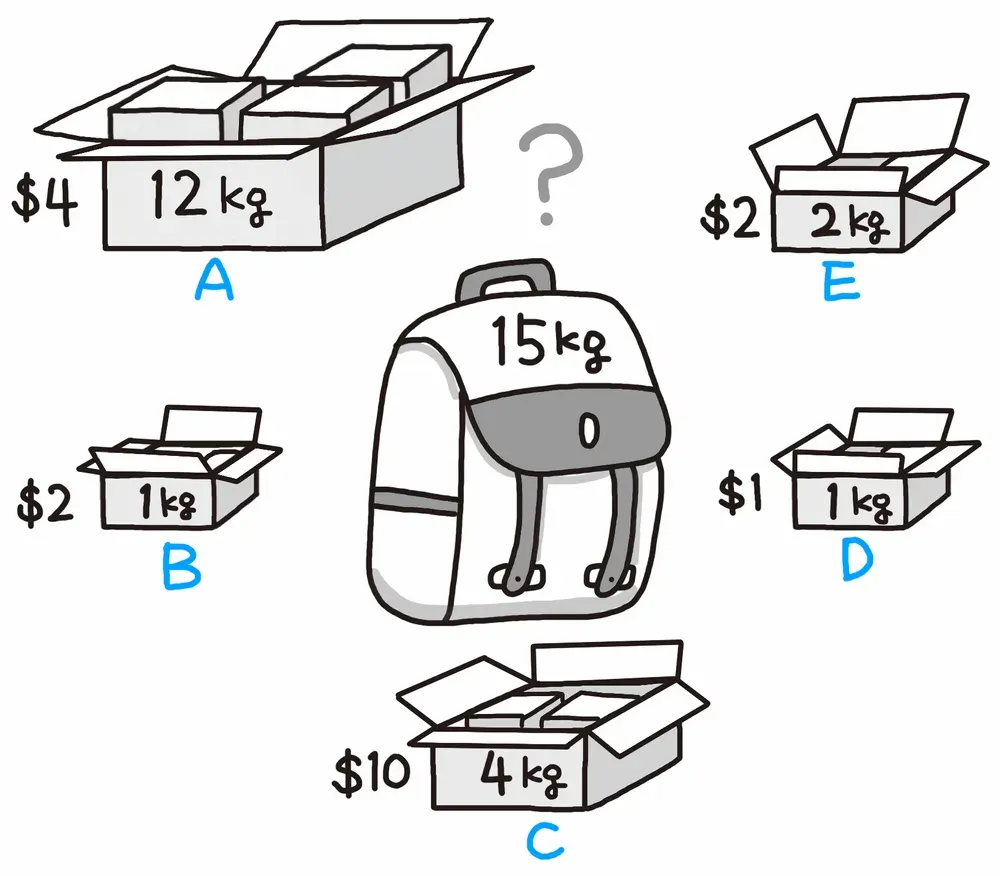
배낭에 담을 수 있는 무게의 최댓값(15kg)이 정해져 있고, 각각 짐의 가치($)와 무게(kg)가 있는 짐들을 배낭에 넣을 때, 가치의 합이 최대가 되도록, 즉 $의 가치가 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.
이 경우, 단가가 가장 높은 짐부터 차례대로 채워나가면 되는데, 이 그림에서는 C의 단가가 2.5달러로 가장 높으므로 C, B, E, D 순으로 총 8kg의 짐을 배낭에 담고 마지막 남은 7kg을 위해 A의 7/12 만큼을 쪼개서 배낭에 담는다. 즉 단가가 높은 순으로 그리디 알고리즘으로 담은 것인데, 이렇게 하면 17.33이라는 최적해를 찾을 수 있다.
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
public class FractionalKnapsackExample {
static class Cargo {
// 가치($)
int price;
// 무게(kg)
int weight;
// 단가($/kg)
float unitPrice;
public Cargo(int price, int weight) {
this.price = price;
this.weight = weight;
}
public void setUnitPrice(float unitPrice) {
this.unitPrice = unitPrice;
}
}
public static float fractionalKnapsack(List<Cargo> cargo) {
// 용량
int capacity = 15;
// 담을 수 있는 최댓값
float totalValue = 0;
// 단가를 계산하여 업데이트
for (Cargo c : cargo) {
c.setUnitPrice((float) c.price / c.weight);
}
// 단가 역순으로 정렬
cargo.sort(Comparator.comparingDouble(a -> a.unitPrice * -1));
// 배낭에 단가 역순으로 담긴 짐의 최댓값 계산
for (Cargo c : cargo) {
// 짐을 쪼개지 않아도 되는 경우 전체 가격 증가
if (capacity - c.weight >= 0) {
capacity -= c.weight;
totalValue += c.price;
} else {
float fraction = (float) capacity / c.weight;
totalValue += c.price * fraction;
break;
}
}
return totalValue;
}
public static void main(String[] args) {
List<Cargo> cargo = new ArrayList<>();
cargo.add(new Cargo(4,12));
cargo.add(new Cargo(2,1));
cargo.add(new Cargo(10,4));
cargo.add(new Cargo(1,1));
cargo.add(new Cargo(2,2));
float result = fractionalKnapsack(cargo); // 17.333334
}
}
Java
복사
동전 바꾸기
또 다른 유명한 문제 중 하나로 동전 바꾸기 문제(Coin-Change Problem)가 있다. 동전의 액면이 10원, 50원, 100원 처럼 증가하면서 이전 액면의 배수 이상이 되면 그리디 알고리즘으로 풀 수 있다. 우리나라 동전은 항상 배수 이상이므로 그리디로 풀 수 있다.
예시로 160원을 거슬러 준다면 10원짜리 16개보다 100원짜리 하나, 50원짜리 하나, 10원짜리 하나로 각각의 동전을 최대한 거슬러주는 그리디한 방법이 가장 적은 동전 개수로 거슬러줄 수 있는 방법이다.
그런데, 다른 나라에 갔더니 80원짜리 동전이 있다면?? 이 경우 더 이상 그리디하게 풀 수 없다. 이 경우 다이나믹 프로그래밍으로 풀어야 한다.