Normalization

목차

<논문 링크>

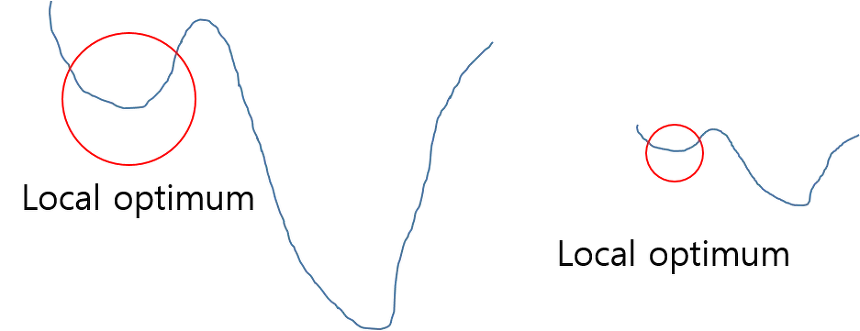
기본적으로 정규화를 하는 이유는 학습을 더 빨리 하기 위해서 or local optimum 문제에 빠지는 가능성을 줄이기 위해서 사용한다. 아래 그림에서 최저점을 찾을 때 그래프를 전체적으로 이해하지 못하여 global optimum 지점을 찾지 못하고 local optimum 에 머물러 있게 되는 문제가 발생하게 된다. 이러한 문제점은 정규화 하여 그래프를 왼쪽에서 오른쪽으로 만들어, local optimum 에 빠질 수 있는 가능성을 낮춰주게 된다.

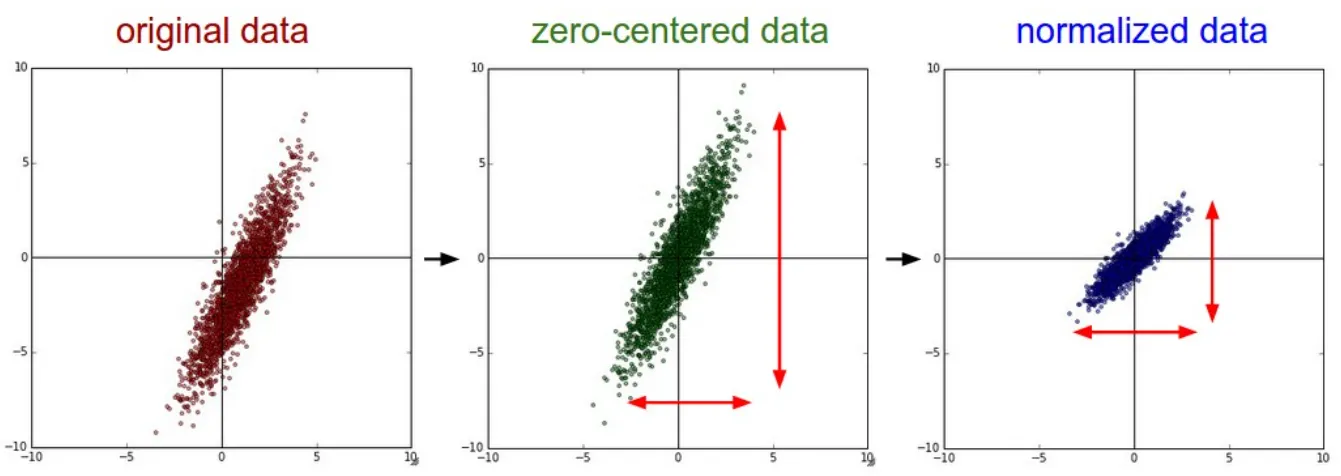
(좌) Normalization 적용 전 / (우) Normalization 적용 후

Internal Convariate Shift

배치 정규화 논문에서는 학습에서 불안정화가 일어나는 이유를 ‘Internal Covariate Shift' 라고 주장하고 있는데, 이는 네트워크의 각 레이어나 Activation 마다 다음 입력값(출력값)의 분산이 달라지는 현상을 뜻한다.

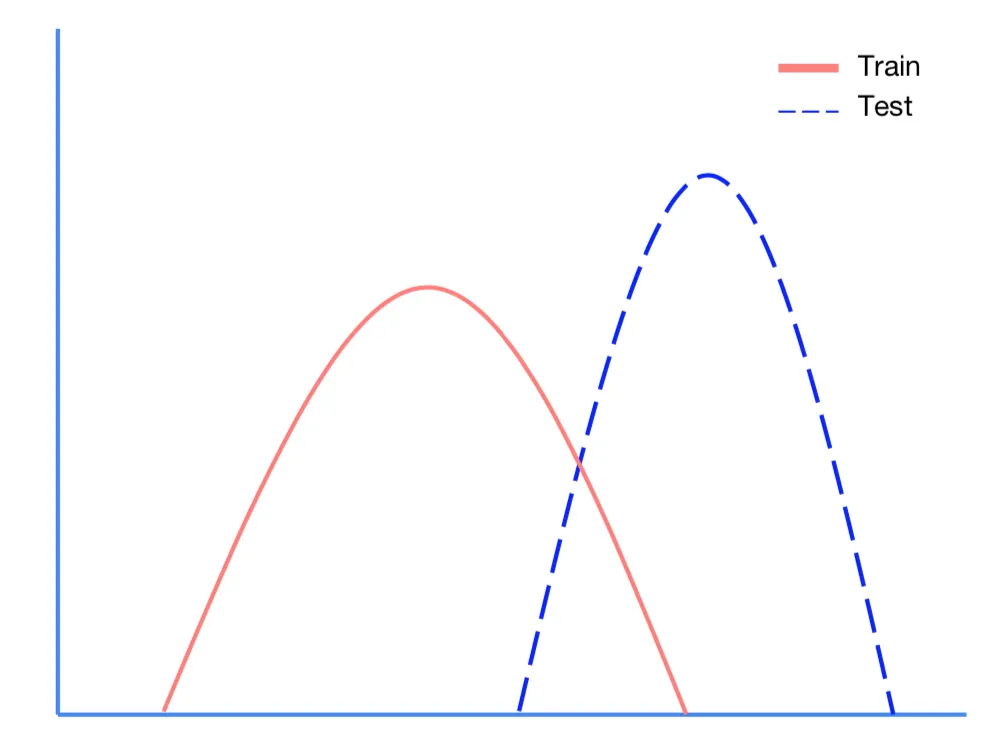
Covariate Shift의 개념 : 학습셋과 검증셋 분포의 차이가 문제를 발생시킴

위 그래프처럼 빨간색 그래프가 train set 파란색이 test set이라고 할 때, 학습셋과 검증셋의 분포(distribution)의 차이가 어떤 문제점을 발생시킨 게 Covariate Shift(공변량 변화)의 개념이다. 입력과 출력의 분포가 다르다는 것도 이와 유사한 개념이다.

Covariate Shift : 이전 레이어의 파라미터 변화로 인하여 현재 레이어의 입력의 분포가 바뀌는 현상
Internal Covariate Shift : 레이어를 통과할 때 마다 Covariate Shift 가 일어나면서 입력의 분포가 약간씩 변하는 현상

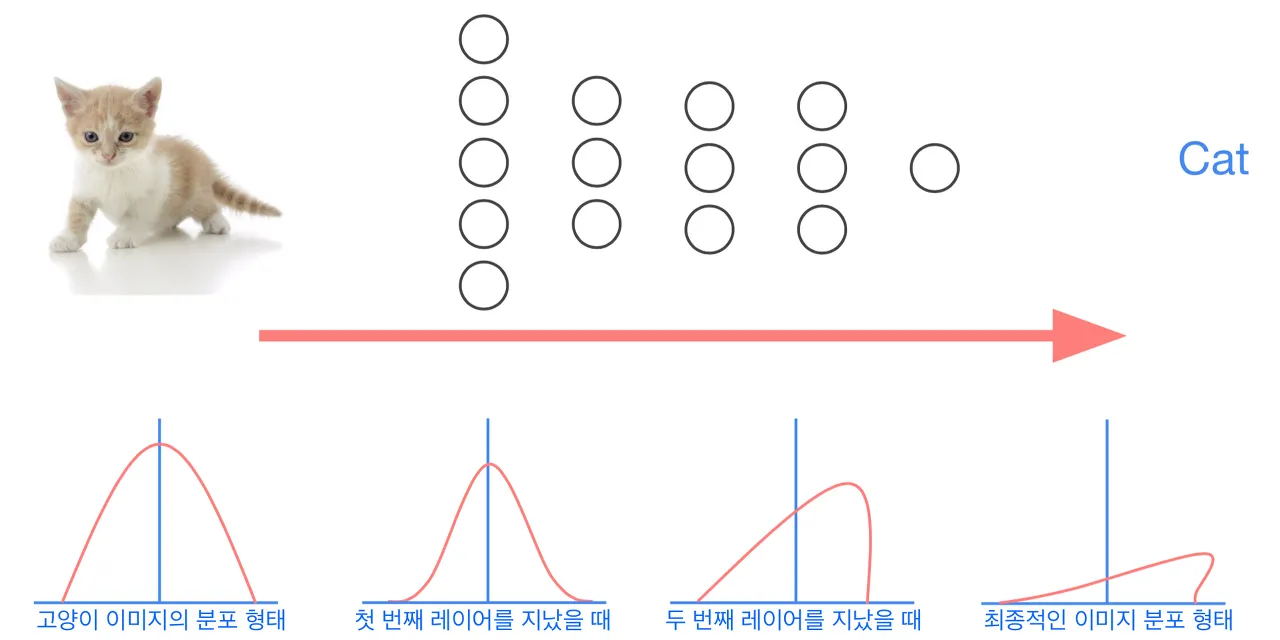
여러 장의 고양이 이미지들은 어떤 분포 형태를 띄고 있으며, forward 되면서 첫 번째 레이어를 통과할 때 covariate shift 문제가 발생한다고 가정해 보자. 1, 2, 3, 4 레이어를 지나면서 분포가 약간씩 변하게 된다. 이러한 현상을 Internal Covariate Shift 라고 한다.

Normalization, Whitening

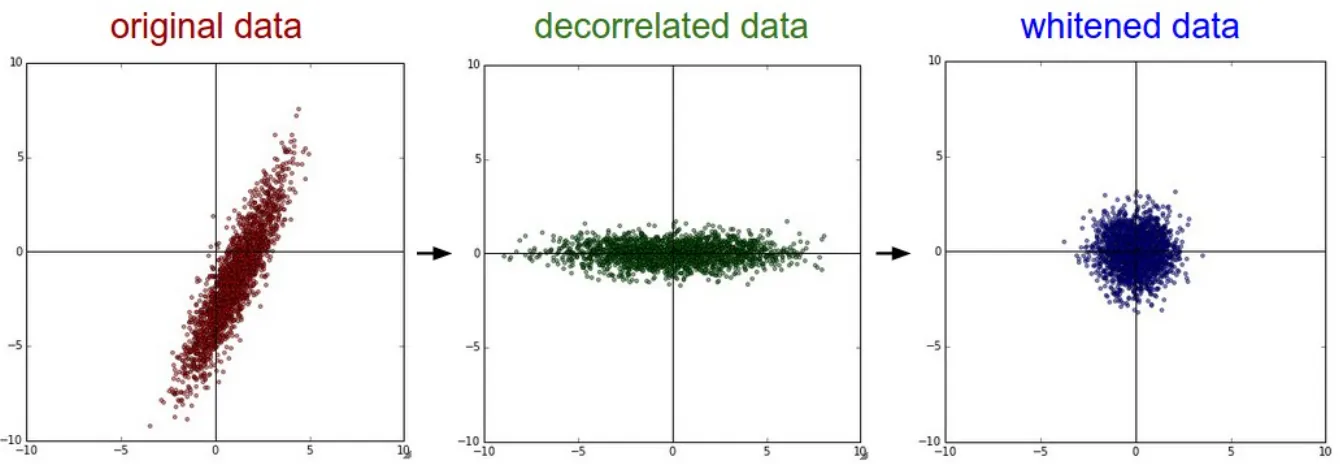
위의 현상을 막는 방법, 즉 다른 분포를 가지는 두 데이터를 같은 분포를 가질 수 있게 변환을 해주는 방법으로 Normalization과 Whitening을 생각해 볼 수 있다.

정규화(Normalization)는 데이터를 동일한 범위 내의 값을 갖도록 하는 기법으로 대표적으로 Min-Max, Standardization이 있다. 이 중에서 Standardization은 데이터를 평균 0, 표준편차 1이 되게 변환하여 정규화시킨다.

화이트닝(Whitening)은 데이터의 평균을 0, 그리고 공분산을 단위행렬(각각의 분산 1)로 갖는 정규분포 형태로 변환하는 기법이다. 그러나 Whitening은 covariance matrix(공분산 행렬) 계산과 inverse(역행렬)의 계산이 필요하기 때문에 계산량이 많을 뿐더러, 이전 레이어로부터 학습이 가능한 파라미터들의 영향을 무시해버린다.

Batch Normalization

이러한 Whitening의 문제점을 해결하도록 한 트릭이 배치 정규화이다.

배치 정규화는 평균과 분산을 조정하는 과정이 별도의 과정으로 떼어진 것이 아니라, 신경망 안에 포함되어 학습 시 평균과 분산을 조정하는 과정 역시 같이 조절된다는 점이 단순 Whitening 과는 구별된다.

즉, 각 레이어마다 정규화 하는 레이어를 두어, 변형된 분포가 나오지 않도록 조절하게 하는 것이 배치 정규화이다.

배치 정규화 알고리즘

배치 정규화는 간단히 말하자면 미니배치의 평균과 분산을 이용해서 정규화 한 뒤에, scale 및 shift 를 감마(

\gamma

) 값, 베타(

\beta

) 값을 통해 실행한다.

이 때 감마와 베타 값은 학습 가능한 변수이다. 즉, Backpropagation을 통해서 학습이 된다.

•

training data 전체를 다 학습할 수 없으므로 일정 크기에 해당하는 mini batch
 안에서 평균과 분산을 계산

→

m

: mini batch의 크기

\mu_B \leftarrow \frac{1}{m}\sum^m_{i=1}x_i

\sigma^2_B \leftarrow \frac{1}{m}\sum^m_{i=1}(x_i-\mu_B)^2

•

입력 데이터에 대하여 각 차원(feature)별로 normalization을 수행

•

epsilon은 계산할 때 0으로 나눠지는 것을 막는, 수치적 안정성 보장을 위한 아주 작은 숫자

\hat{x_i} \leftarrow \frac{x_i-\mu_B}{\sqrt{\sigma^2_B+\epsilon}}

•

normalization 된 값들에 대해 Scale factor(γ\gammaγ)와 Shift factor(β\betaβ)를 더하여 학습이 가능한 파라미터를 추가함

y_i \leftarrow \gamma\hat{x}_i + \beta \equiv BN_{\gamma,\beta}(x_i)

Scale factor와 Shift factor를 두게 되면 입력 데이터의 원래 형태(normalization 하기 전)로도 학습이 가능하여 각 층별로 입력 데이터의 optimal uncorrelated distribution을 구할 수 있게 된다.

또 Sigmoid와 같은 활성화 함수에서 비선형성을 잃어버리는 것을 방지할 수 있다. 정규화 이후에 사용되는 두 factors가 학습됨에 따라 non-linearity를 유지하도록 해준다.

따라서 BN은 학습 가능한 parameters가 존재하는 하나의 레이어 구조가 되며 이 기법이 발표된 이후 기존의 딥러닝 구조에서 Convolution Layer와 Activation Layer 사이에 BN Layer가 들어간 형태로 발전했다. 이 구조로 성능 효과를 크게 높이게 되어 거의 모든 딥러닝 구조에 BN기법이 사용되기 시작했다.

Batch Normalization Architecture

Batch size와의 연관성

•

batch의 크기가 너무 작으면 잘 동작하지 않음

◦

GPU 메모리의 한계로 인해 RNN이나 크기가 큰 CNN에 적용하기가 어려움.

◦

큰수의 법칙과 중심 극한 이론을 만족하지 못하기에 평균과 표준편차가 데이터 전체 분포를 잘 표현하지 못함.

•

batch의 크기가 너무 커져도 잘 동작하지 않음

◦

적절한 크기의 샘플은 중심 극한 이론을 통해 적절한 정규분포를 따르게 되나, 너무 큰 샘플을 사용한 경우 multi model 형태의 gaussian mixture 모델 형태가 나타날 수 있기 때문.

◦

gradiant를 계산하는 기준이 Batch 단위인데, gradient를 계산을 너무 한번에 하게 되어 학습에도 악영향 있음.

RNN과의 연관성

RNN에서는 각 단계마다 서로 다른 통계치를 가진다. 따라서 매 단계마다 레이어에 별도의 BN을 적용해야한다. 이는 모델을 더 복잡하게 만들며, 계속 새롭게 형성된 통계치를 저장해야한다는 것을 말한다. 이러한 상황에서 BN은 매우 비효율적인 방법이다.

위와 같은 Batch Normalization의 한계를 개선하기 위하여 Weight Normalization이나, Layer Normalization 등이 사용되기도 한다.

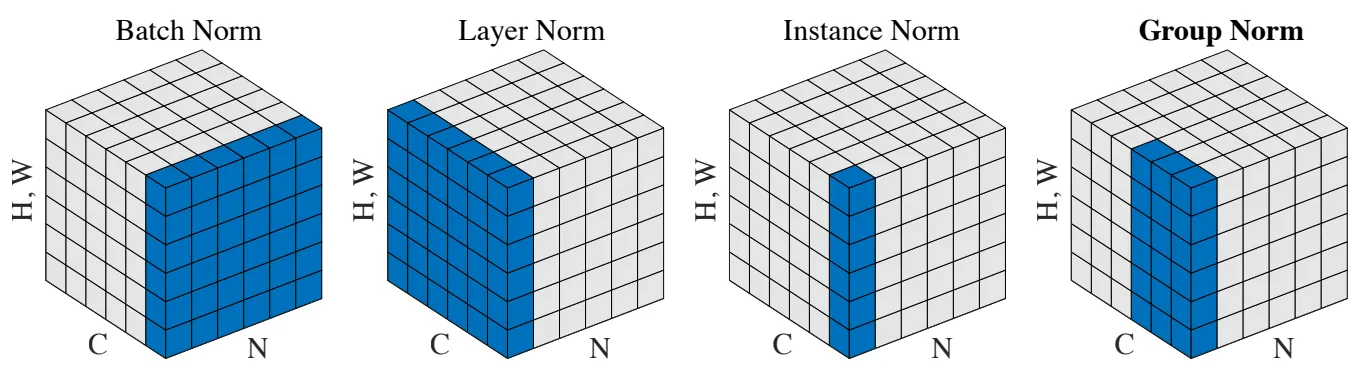
Normalization methods

Weight Normalization

Layer Normalization

Instance Normalization

Group Normalization

Inference with Batch Normalization

학습시에는 mini batch의 평균과 분산을 이용했지만, inference 혹은 test 시에는 이를 이용할 수 없다. inference 시 입력되는 데이터의 평균과 분산을 이용하면 배치 정규화가 온전하게 이루어지지 않는다.

애초에 배치 정규화를 통해 수행하고자 하는 것이 학습되는 동안 모델이 추정한 입력 데이터 분포의 평균과 분산으로 정규화를 하고자 하는 것인데, inference시에 입력되는 값을 통해서 정규화를 하게 되면 모델이 학습을 통해서 입력 데이터의 분포를 추정하는 의미 자체가 없어지게 된다.

inference 에서는 결과를 Deterministic 하게 하기 위하여, 고정된 평균과 분산을 이용하여 정규화를 수행하게 되기 때문이다.

이러한 문제를 미리 저장해둔 미니 배치의 이동 평균(Moving Average)을 사용하여 해결한다. 즉, inference 전에 학습 시에 미리 미니 배치를 뽑을 때 Sample Mean 및 Sample Variance 를 이용하여 각각의 이동 평균을 구해놔야한다.

입력값	100	110	130	120	140	110	130
이동평균	100	105	120	125	130	125	120

길이가 2인 경우의 이동 평균 예시는 다음과 같다. 처음엔 값이 100 하나 밖에 없기 때문에 이동 평균이 100이지만, 값이 업데이트 됨에 따라 가장 최근 2개 정보만을 통해 평균을 구한 것이 길이가 2인 경우의 이동 평균이다.

Batch Normalization의 Inference시 Moving Average 계산 식