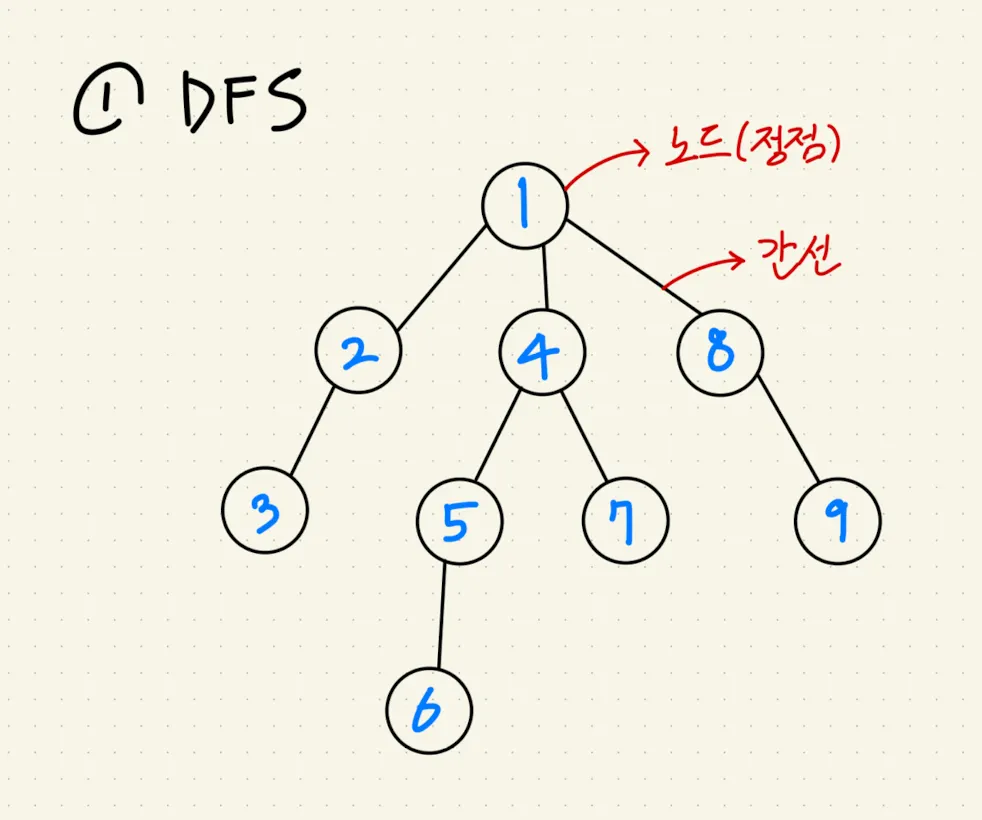
DFS - 깊이 우선 탐색 / BFS - 너비 우선 탐색
•
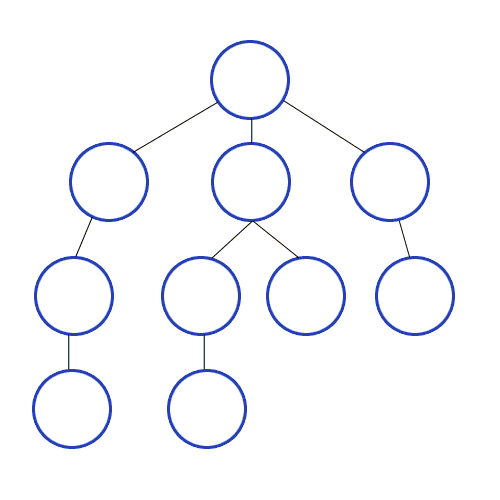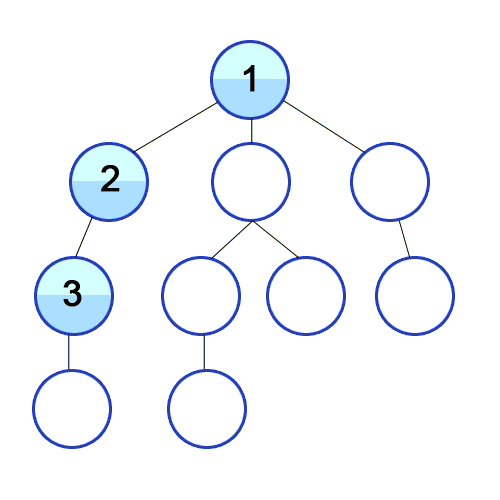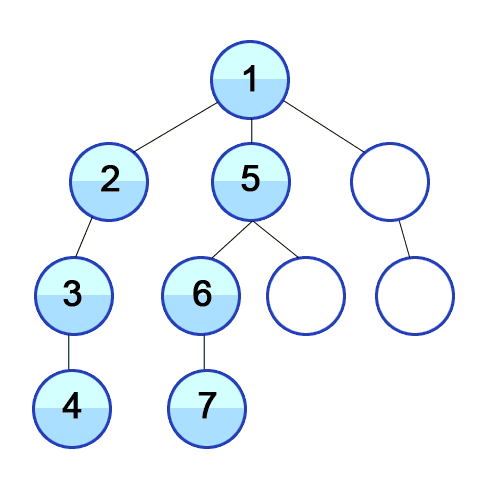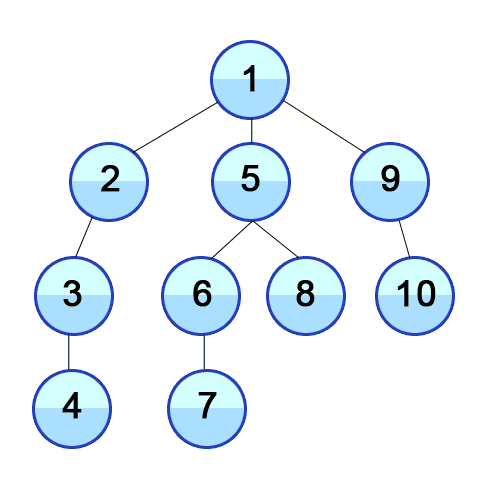
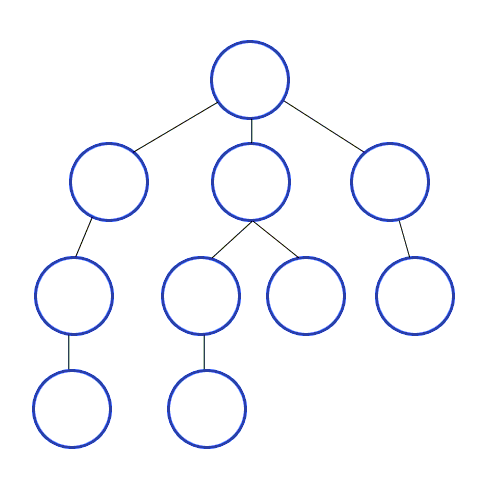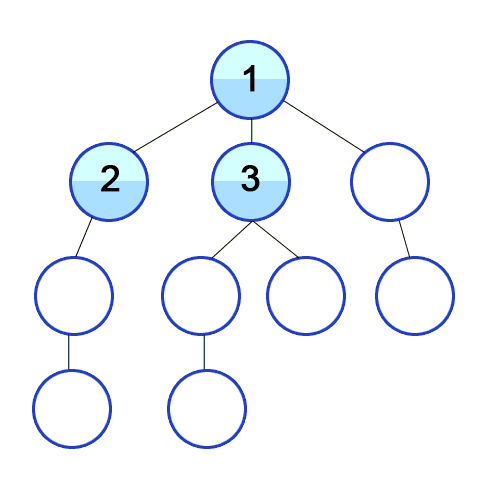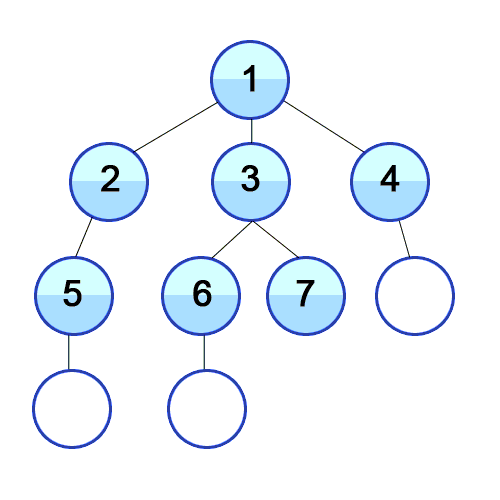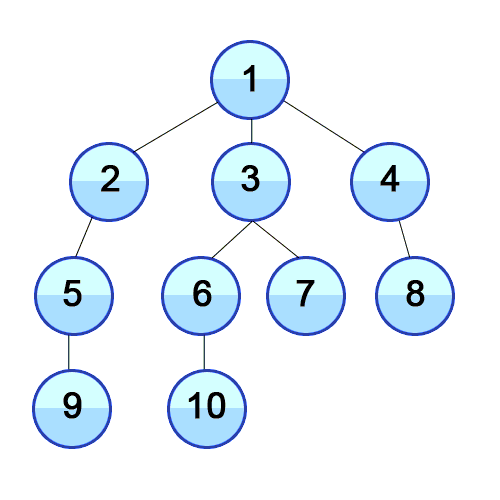
DFS(Depth First Search)
•
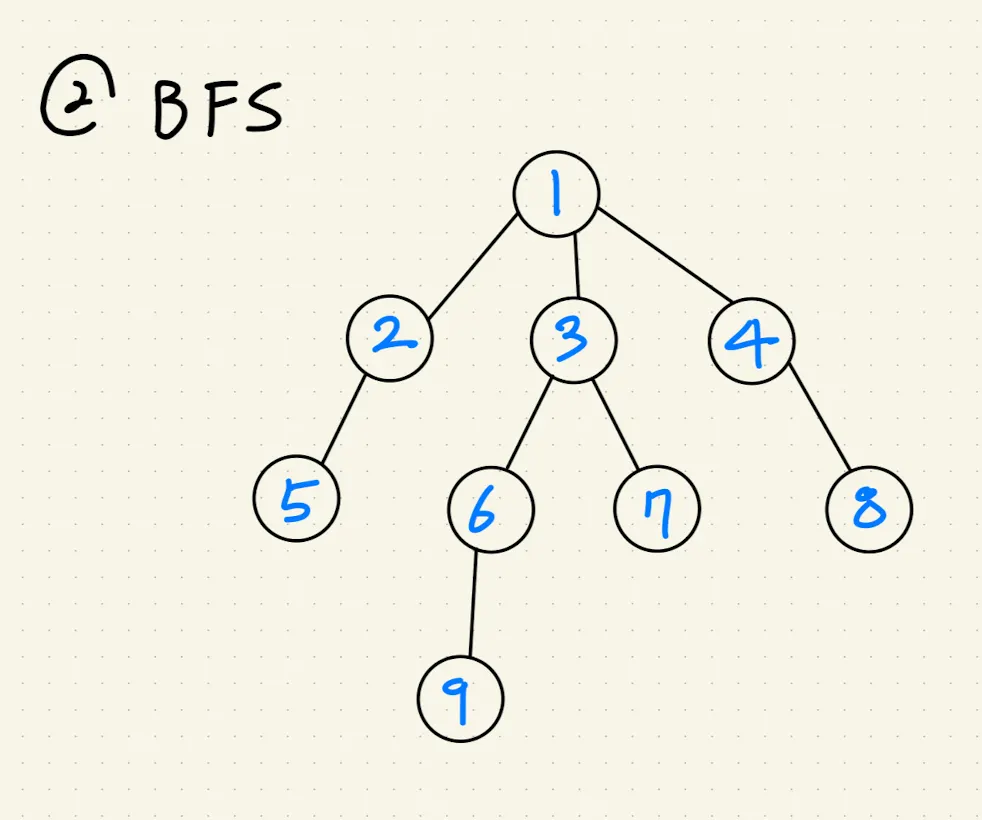
BFS(Breadth First Search)
1) 방문 리스트 : 방문 처리 목적 / 정점의 개수만큼 길이 생성
visited = [0] * 정점의 개수
2) 인접 행렬 / 인접 리스트 : 노드, 간선 연결 저장
3) stack / queue : 실시간 현황
자료구조 : 스택 (후입선출)
1.
루트 노드를 스택에 넣고 방문 처리 한다.
2.
스택 최상단 노드의 인접 노드 중 방문하지 않은 노드 하나를 스택에 넣고 방문 처리한다. 만약 인접 노드를 모두 방문한 경우 스택을 Pop 한다.
3.
2 단계를 더 이상 수행할 수 없을 때 까지 (스택이 빌 때 까지) 반복한다.
자료구조 : 큐 (선입선출)
1.
루트 노드를 큐에 넣고 방문 처리한다.
2.
방문 처리한 노드를 큐에서 제거하고, 제거한 노드의 방문하지 않은 모든 인접 노드를 큐에 넣고 방문 처리한다.
3.
2 단계를 더 이상 수행할 수 없을 때 까지 (큐가 빌 때 까지) 반복한다.
DFS / BFS 예제
•
DFS 예제
# DFS 메서드 정의
def dfs(graph, v, visited):
#현재 노드를 방문 처리
visited[v] = True
print(v, end=' ')
# 현재 노드와 연결된 자식 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
dfs(graph, 1, visited)
# 출력
1 2 7 6 8 3 4 5
Python
복사
•
BFS 예제
from collections import deque
# BFS 메서드 정의
def bfs(graph, start, visited):
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque([start])
# 현재 노드를 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v, end = " ")
# 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False]*9
bfs(graph, 1, visited)
# 출력
1 2 3 8 7 4 5 6
Python
복사
인접 행렬 / 인접 리스트
1) 인접 행렬 : 행렬로 정점들 사이의 관계를 표현하는 방식
2) 인접 리스트 : 각 정점에 연결된 노드들의 정보를 저장하는 방식
•
시간복잡도
◦
인접 리스트 : O(V + E)
◦
인접 행렬 : O(V^2)
/* 인접 리스트 이용 */
class Graph {
private int V;
private LinkedList<Integer> adj[];
Graph(int v) {
V = v;
adj = new LinkedList[v];
// 인접 리스트 초기화
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
void addEdge(int v, int w) { adj[v].add(w); }
/* DFS에 의해 사용되는 함수 */
void DFSUtil(int v, boolean visited[]) {
// 현재 노드를 방문한 것으로 표시하고 값을 출력
visited[v] = true;
System.out.print(v + " ");
// 방문한 노드와 인접한 모든 노드를 가져온다.
Iterator<Integer> it = adj[v].listIterator();
while (it.hasNext()) {
int n = it.next();
// 방문하지 않은 노드면 해당 노드를 시작 노드로 다시 DFSUtil 호출
if (!visited[n])
DFSUtil(n, visited);
}
}
/* DFS */
void DFS(int v) {
boolean visited[] = new boolean[V];
// v를 시작 노드로 DFSUtil 재귀 호출
DFSUtil(v, visited);
}
}
Java
복사
class Graph {
private int V;
private LinkedList<Integer> adj[];
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
void addEdge(int v, int w) { adj[v].add(w); }
/* BFS */
void BFS(int s) {
boolean visited[] = new boolean[V];
LinkedList<Integer> queue = new LinkedList<Integer>();
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
// 방문한 노드를 큐에서 추출(dequeue)하고 값을 출력
s = queue.poll();
System.out.print(s + " ");
// 방문한 노드와 인접한 모든 노드를 가져온다.
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
// 방문하지 않은 노드면 방문한 것으로 표시하고 큐에 삽입(enqueue)
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
Java
복사